When Random Tensors meet Random Matrices
Paper and Code
Jan 12, 2022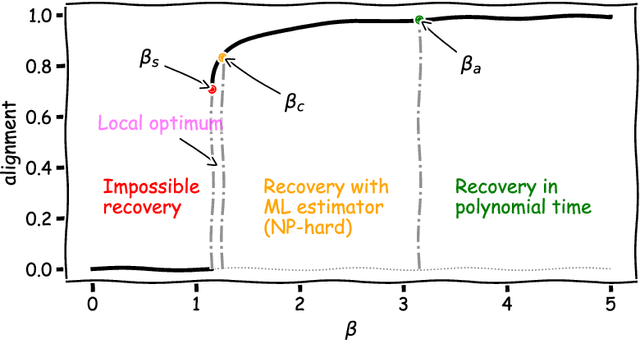
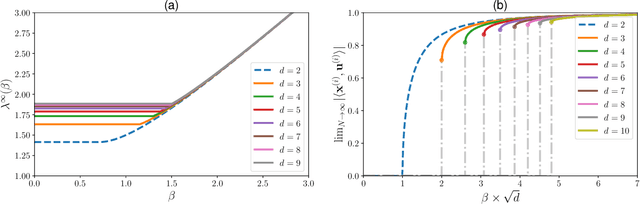
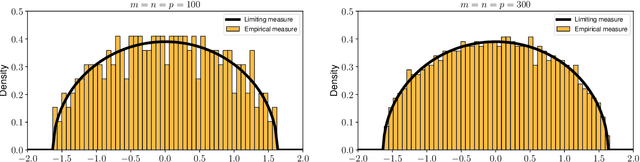
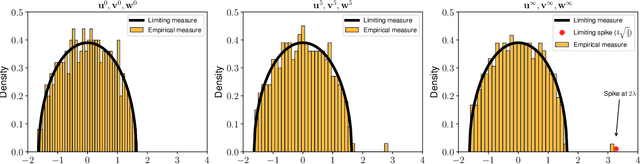
Relying on random matrix theory (RMT), this paper studies asymmetric order-$d$ spiked tensor models with Gaussian noise. Using the variational definition of the singular vectors and values of (Lim, 2005), we show that the analysis of the considered model boils down to the analysis of an equivalent spiked symmetric block-wise random matrix, that is constructed from contractions of the studied tensor with the singular vectors associated to its best rank-1 approximation. Our approach allows the exact characterization of the almost sure asymptotic singular value and alignments of the corresponding singular vectors with the true spike components, when $\frac{n_i}{\sum_{j=1}^d n_j}\to c_i\in [0, 1]$ with $n_i$'s the tensor dimensions. In contrast to other works that rely mostly on tools from statistical physics to study random tensors, our results rely solely on classical RMT tools such as Stein's lemma. Finally, classical RMT results concerning spiked random matrices are recovered as a particular case.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge