When does gradient descent with logistic loss find interpolating two-layer networks?

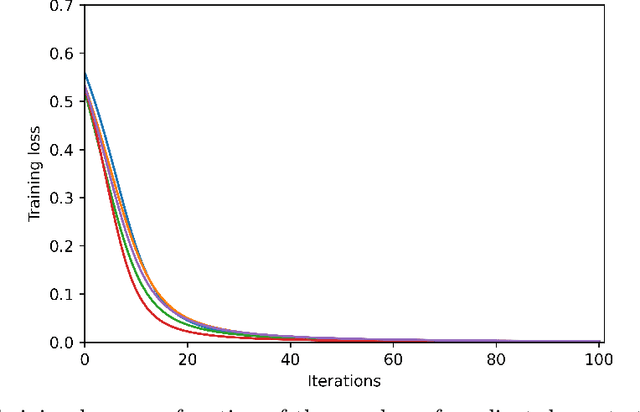
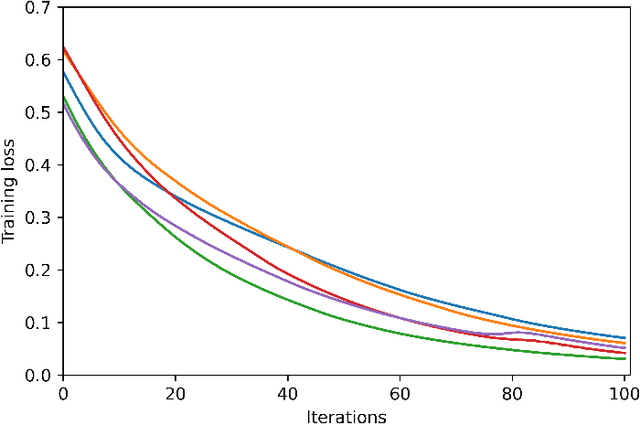
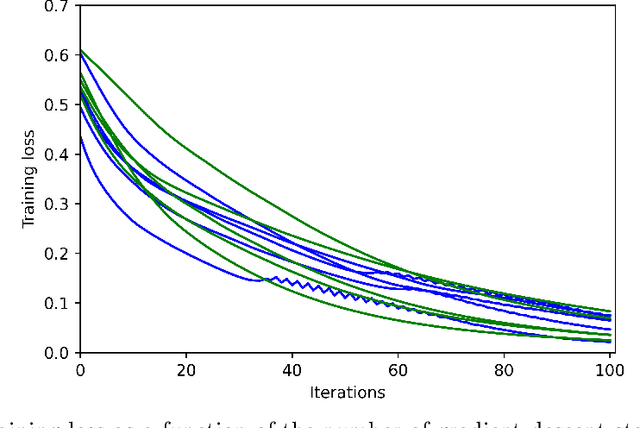
We study the training of finite-width two-layer smoothed ReLU networks for binary classification using the logistic loss. We show that gradient descent drives the training loss to zero if the initial loss is small enough. When the data satisfies certain cluster and separation conditions and the network is wide enough, we show that one step of gradient descent reduces the loss sufficiently that the first result applies. In contrast, all past analyses of fixed-width networks that we know do not guarantee that the training loss goes to zero.