When can we improve on sample average approximation for stochastic optimization?
Paper and Code
Jul 19, 2019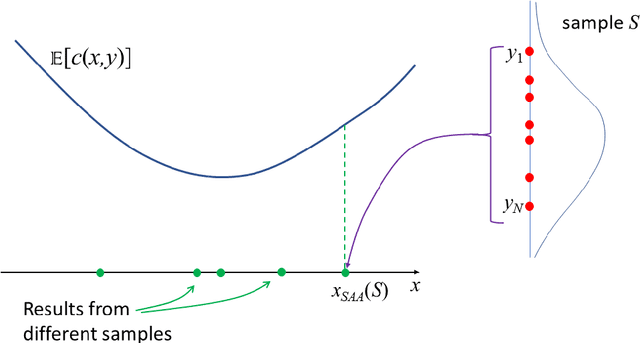
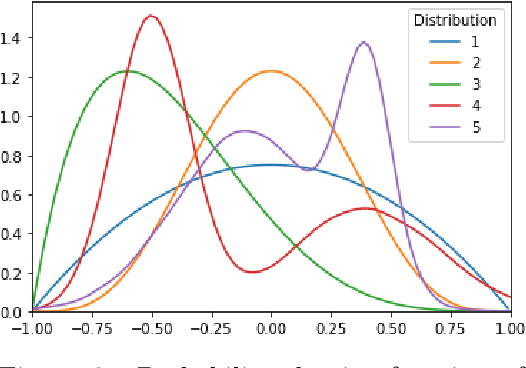
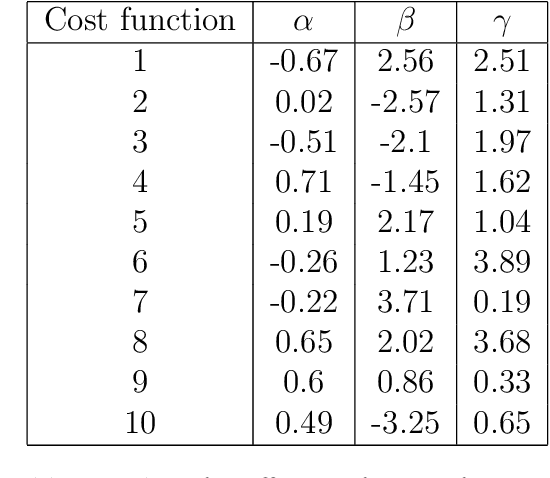
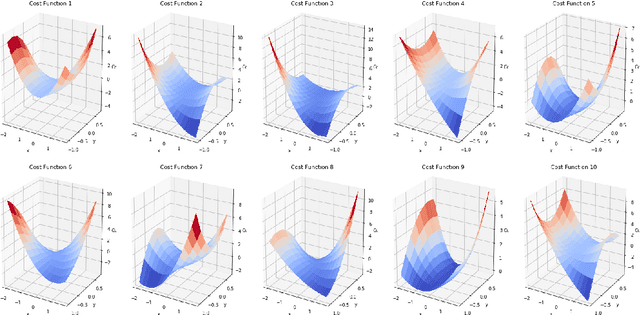
We explore the performance of sample average approximation in comparison with several other methods for stochastic optimization when there is information available on the underlying true probability distribution. The methods we evaluate are (a) bagging; (b) kernel smoothing; (c) maximum likelihood estimation (MLE); and (d) a Bayesian approach. We use two test sets, the first has a quadratic objective function allowing for very different types of interaction between the random component and the univariate decision variable. Here the sample average approximation is remarkably effective and only consistently outperformed by a Bayesian approach. The second test set is a portfolio optimization problem in which we use different covariance structures for a set of 5 stocks. Here bagging, MLE and a Bayesian approach all do well.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge