What Makes the Game of Life Special?

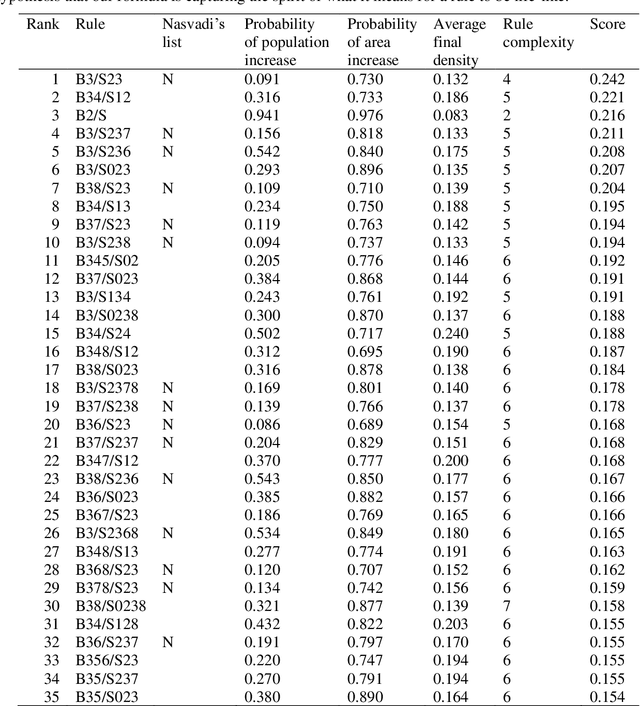
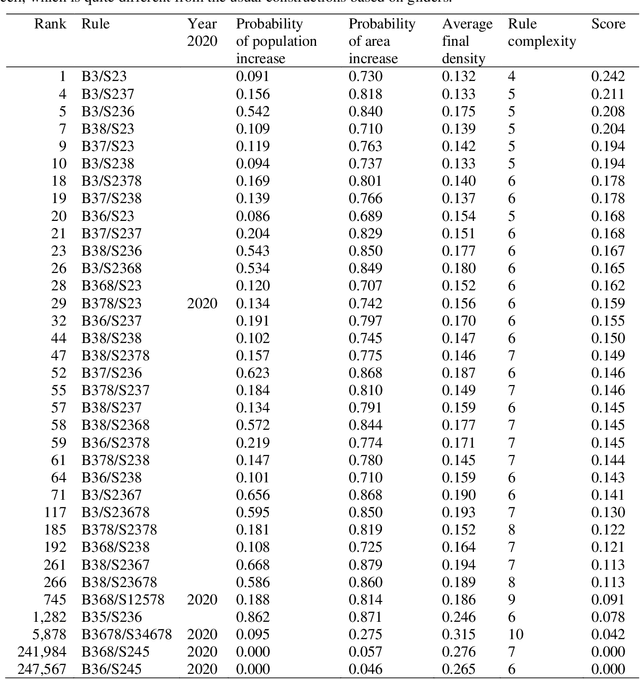
Conway's Game of Life (GoL) is the best-known cellular automaton. It is a classic model of emergence and self-organization, it is Turing-complete, and it can simulate a universal constructor. GoL belongs to the set of semi-totalistic cellular automata, a family with 262,144 members. In such a large family, what makes GoL stand out? Packard and Wolfram (1985) proposed a set of four qualitative classes for cellular automata. Eppstein (2010) proposed four objective classes. Both classification systems are interesting, but neither can distinguish GoL from its many near relatives. Instead of a classification system, we present a simple and objective metric that assigns a numerical score to all semi-totalistic cellular automata. The metric uses four properties to distinguish GoL from its relatives: GoL is evenly balanced between growth and decay, measured by (1) the number of living cells and (2) the area covered by the living cells; (3) the rule for GoL is simple; and (4) GoL has low density, measured by living cells per area. We combine these four properties in a simple mathematical expression. When we score the 262,144 semi-totalistic cellular automata with this formula, GoL achieves the maximum score. We show that the metric favours Turing-complete automata, although it was not designed to do so, which suggests it captures the spirit of the Game of Life.