Weighted Combinatorial Laplacian and its Application to Coverage Repair in Sensor Networks
Paper and Code
Dec 08, 2023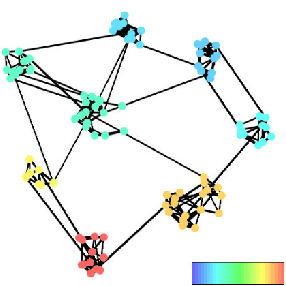
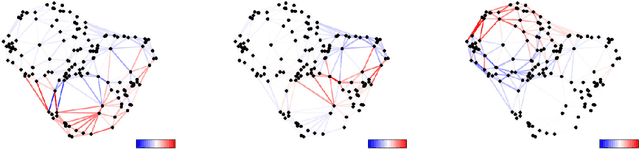
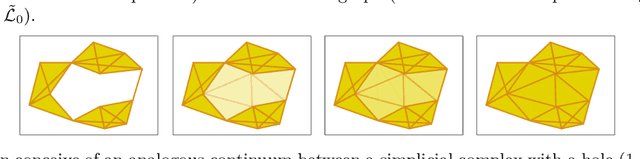
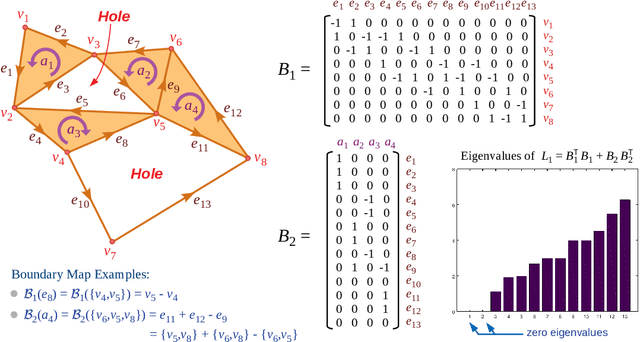
We define the weighted combinatorial Laplacian operators on a simplicial complex and investigate their spectral properties. Eigenvalues close to zero and the corresponding eigenvectors of them are especially of our interest, and we show that they can detect almost $n$-dimensional holes in the given complex. Real-valued weights on simplices allow gradient descent based optimization, which in turn gives an efficient dynamic coverage repair algorithm for the sensor network of a mobile robot team.
* 18 pages, 8 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge