Weighted Aggregation of Conformity Scores for Classification
Paper and Code
Jul 14, 2024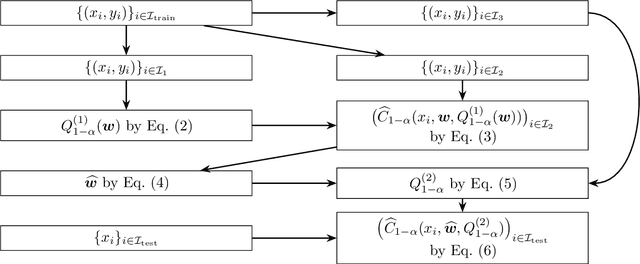
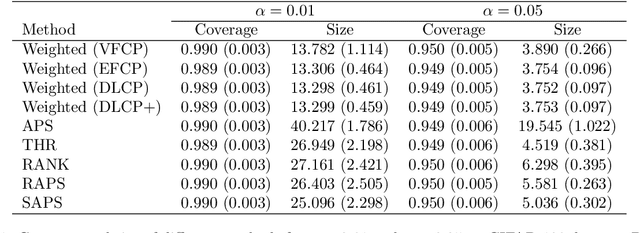
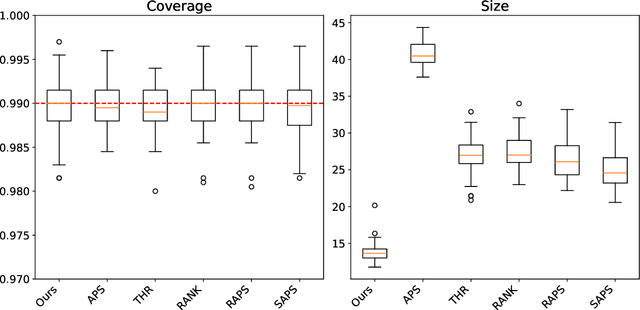
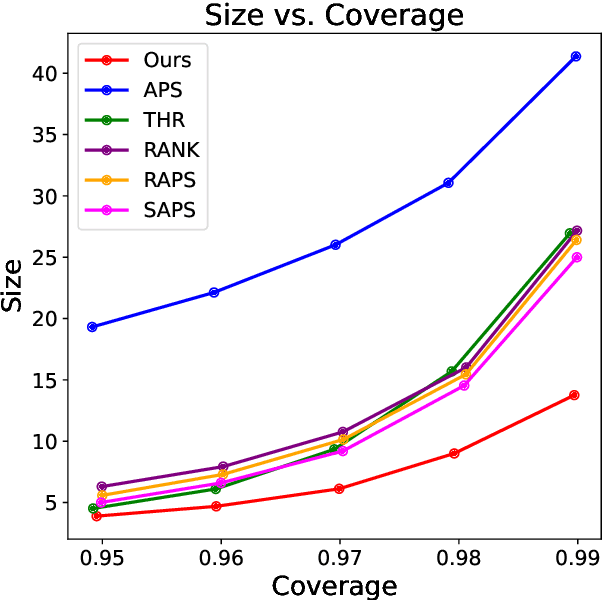
Conformal prediction is a powerful framework for constructing prediction sets with valid coverage guarantees in multi-class classification. However, existing methods often rely on a single score function, which can limit their efficiency and informativeness. We propose a novel approach that combines multiple score functions to improve the performance of conformal predictors by identifying optimal weights that minimize prediction set size. Our theoretical analysis establishes a connection between the weighted score functions and subgraph classes of functions studied in Vapnik-Chervonenkis theory, providing a rigorous mathematical basis for understanding the effectiveness of the proposed method. Experiments demonstrate that our approach consistently outperforms single-score conformal predictors while maintaining valid coverage, offering a principled and data-driven way to enhance the efficiency and practicality of conformal prediction in classification tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge