Verification of Neural-Network Control Systems by Integrating Taylor Models and Zonotopes
Paper and Code
Dec 16, 2021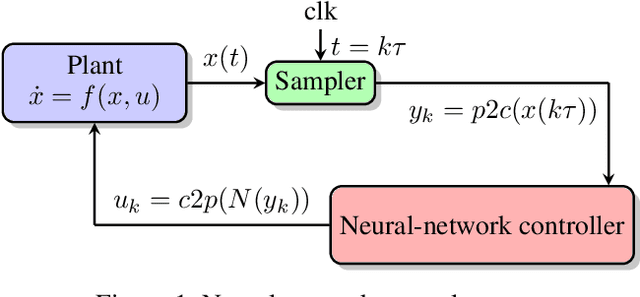
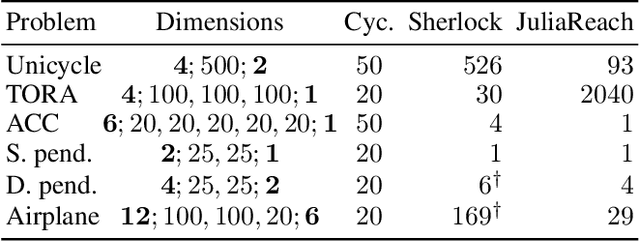

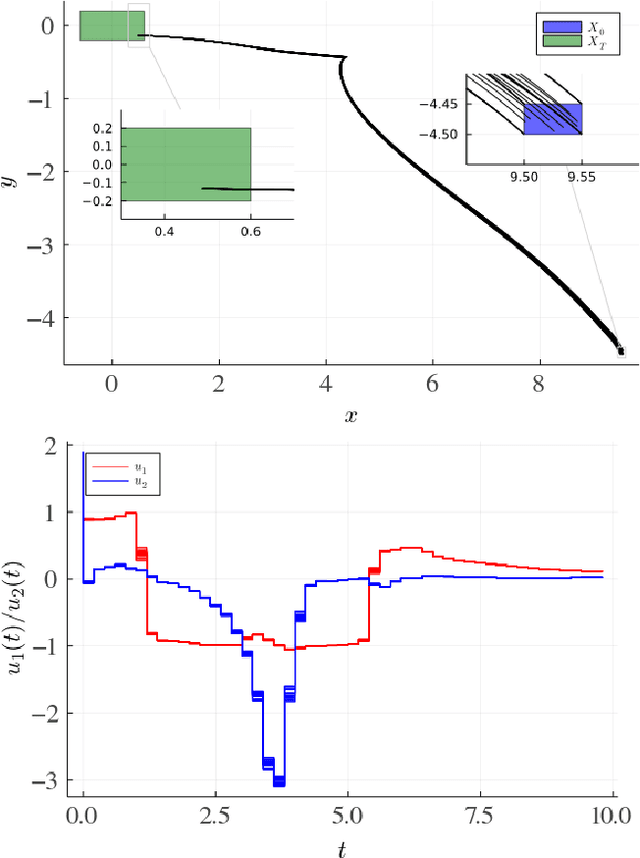
We study the verification problem for closed-loop dynamical systems with neural-network controllers (NNCS). This problem is commonly reduced to computing the set of reachable states. When considering dynamical systems and neural networks in isolation, there exist precise approaches for that task based on set representations respectively called Taylor models and zonotopes. However, the combination of these approaches to NNCS is non-trivial because, when converting between the set representations, dependency information gets lost in each control cycle and the accumulated approximation error quickly renders the result useless. We present an algorithm to chain approaches based on Taylor models and zonotopes, yielding a precise reachability algorithm for NNCS. Because the algorithm only acts at the interface of the isolated approaches, it is applicable to general dynamical systems and neural networks and can benefit from future advances in these areas. Our implementation delivers state-of-the-art performance and is the first to successfully analyze all benchmark problems of an annual reachability competition for NNCS.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge