Variational Wasserstein Clustering
Paper and Code
Jul 26, 2018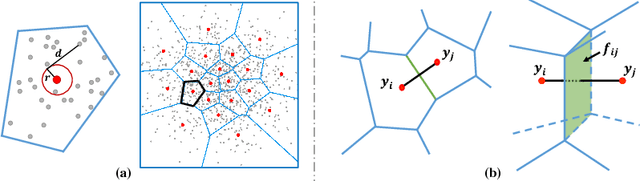


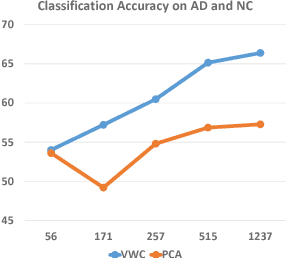
We propose a new clustering method based on optimal transportation. We solve optimal transportation with variational principles, and investigate the use of power diagrams as transportation plans for aggregating arbitrary domains into a fixed number of clusters. We iteratively drive centroids through target domains while maintaining the minimum clustering energy by adjusting the power diagrams. Thus, we simultaneously pursue clustering and the Wasserstein distances between the centroids and the target domains, resulting in a measure-preserving mapping. We demonstrate the use of our method in domain adaptation, remeshing, and representation learning on synthetic and real data.
* Accepted to ECCV 2018
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge