Variational methods for simulation-based inference
Paper and Code
Mar 15, 2022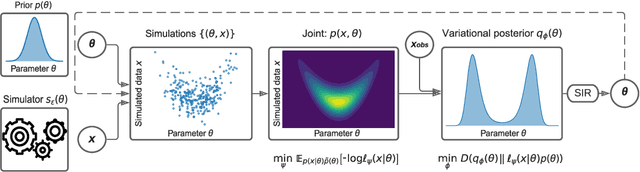

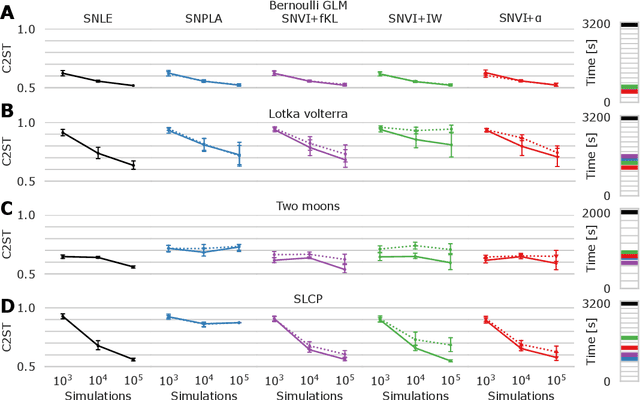
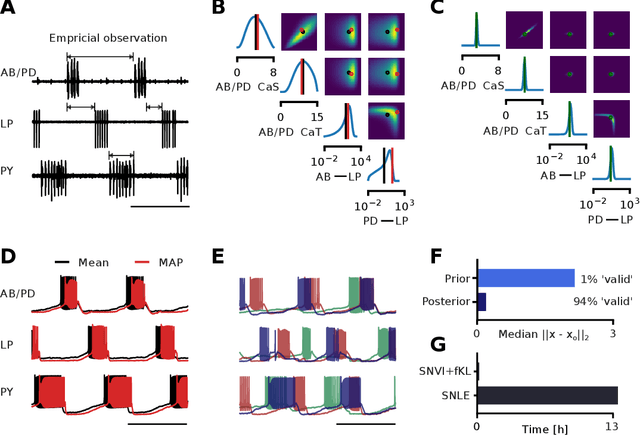
We present Sequential Neural Variational Inference (SNVI), an approach to perform Bayesian inference in models with intractable likelihoods. SNVI combines likelihood-estimation (or likelihood-ratio-estimation) with variational inference to achieve a scalable simulation-based inference approach. SNVI maintains the flexibility of likelihood(-ratio) estimation to allow arbitrary proposals for simulations, while simultaneously providing a functional estimate of the posterior distribution without requiring MCMC sampling. We present several variants of SNVI and demonstrate that they are substantially more computationally efficient than previous algorithms, without loss of accuracy on benchmark tasks. We apply SNVI to a neuroscience model of the pyloric network in the crab and demonstrate that it can infer the posterior distribution with one order of magnitude fewer simulations than previously reported. SNVI vastly reduces the computational cost of simulation-based inference while maintaining accuracy and flexibility, making it possible to tackle problems that were previously inaccessible.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge