Variational Intrinsic Control Revisited

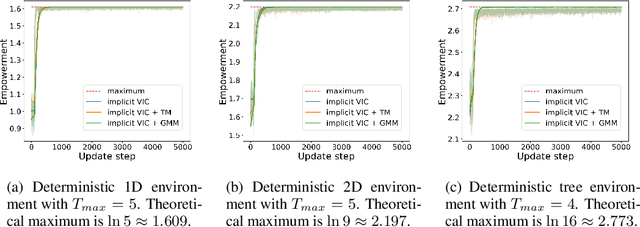
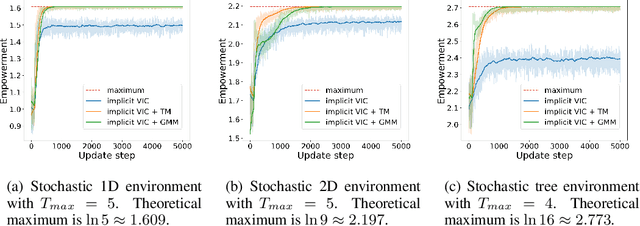
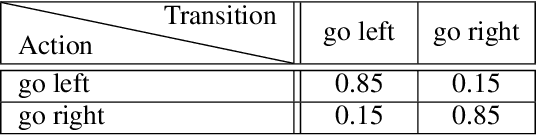
In this paper, we revisit variational intrinsic control (VIC), an unsupervised reinforcement learning method for finding the largest set of intrinsic options available to an agent. In the original work by Gregor et al. (2016), two VIC algorithms were proposed: one that represents the options explicitly, and the other that does it implicitly. We show that the intrinsic reward used in the latter is subject to bias in stochastic environments, causing convergence to suboptimal solutions. To correct this behavior, we propose two methods respectively based on the transitional probability model and Gaussian Mixture Model. We substantiate our claims through rigorous mathematical derivations and experimental analyses.