Variance-Based Rewards for Approximate Bayesian Reinforcement Learning
Paper and Code
Mar 15, 2012
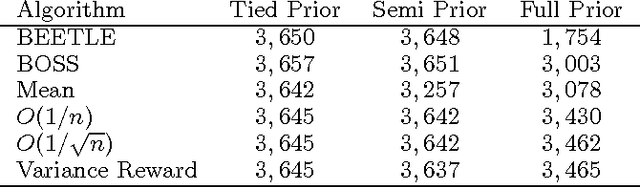
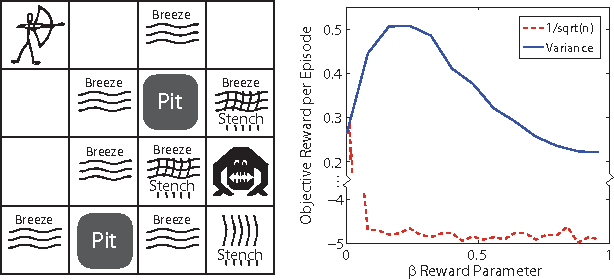

The explore{exploit dilemma is one of the central challenges in Reinforcement Learning (RL). Bayesian RL solves the dilemma by providing the agent with information in the form of a prior distribution over environments; however, full Bayesian planning is intractable. Planning with the mean MDP is a common myopic approximation of Bayesian planning. We derive a novel reward bonus that is a function of the posterior distribution over environments, which, when added to the reward in planning with the mean MDP, results in an agent which explores efficiently and effectively. Although our method is similar to existing methods when given an uninformative or unstructured prior, unlike existing methods, our method can exploit structured priors. We prove that our method results in a polynomial sample complexity and empirically demonstrate its advantages in a structured exploration task.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge