Using Laplacian Spectrum as Graph Feature Representation
Paper and Code
Dec 02, 2019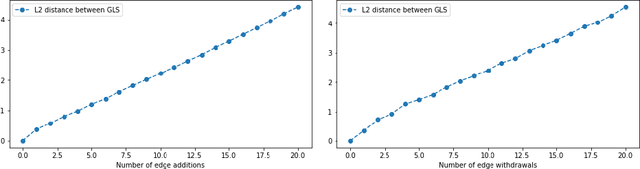
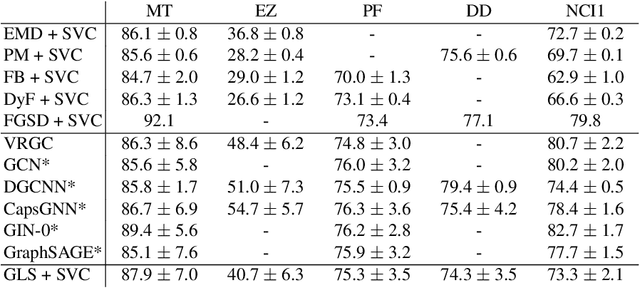
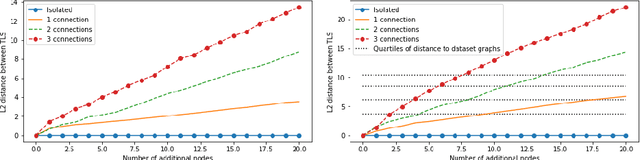

Graphs possess exotic features like variable size and absence of natural ordering of the nodes that make them difficult to analyze and compare. To circumvent this problem and learn on graphs, graph feature representation is required. A good graph representation must satisfy the preservation of structural information, with two particular key attributes: consistency under deformation and invariance under isomorphism. While state-of-the-art methods seek such properties with powerful graph neural-networks, we propose to leverage a simple graph feature: the graph Laplacian spectrum (GLS). We first remind and show that GLS satisfies the aforementioned key attributes, using a graph perturbation approach. In particular, we derive bounds for the distance between two GLS that are related to the \textit{divergence to isomorphism}, a standard computationally expensive graph divergence. We finally experiment GLS as graph representation through consistency tests and classification tasks, and show that it is a strong graph feature representation baseline.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge