Using Bayesian Network Representations for Effective Sampling from Generative Network Models
Paper and Code
Jul 11, 2015
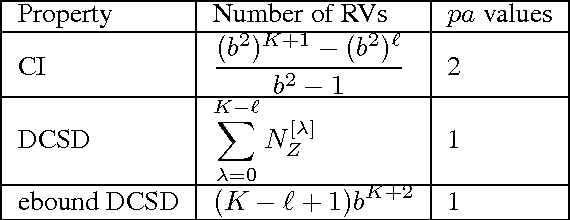

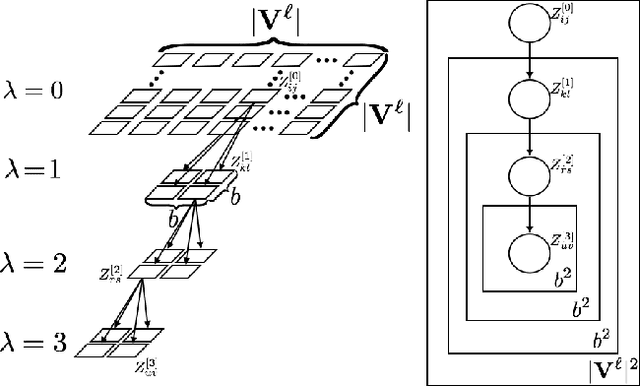
Bayesian networks (BNs) are used for inference and sampling by exploiting conditional independence among random variables. Context specific independence (CSI) is a property of graphical models where additional independence relations arise in the context of particular values of random variables (RVs). Identifying and exploiting CSI properties can simplify inference. Some generative network models (models that generate social/information network samples from a network distribution P(G)), with complex interactions among a set of RVs, can be represented with probabilistic graphical models, in particular with BNs. In the present work we show one such a case. We discuss how a mixed Kronecker Product Graph Model can be represented as a BN, and study its BN properties that can be used for efficient sampling. Specifically, we show that instead of exhibiting CSI properties, the model has deterministic context-specific dependence (DCSD). Exploiting this property focuses the sampling method on a subset of the sampling space that improves efficiency.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge