Unimodal Mono-Partite Matching in a Bandit Setting
Paper and Code
Aug 02, 2022
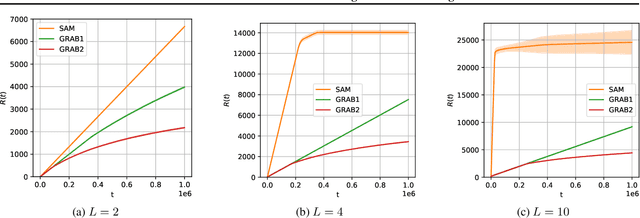

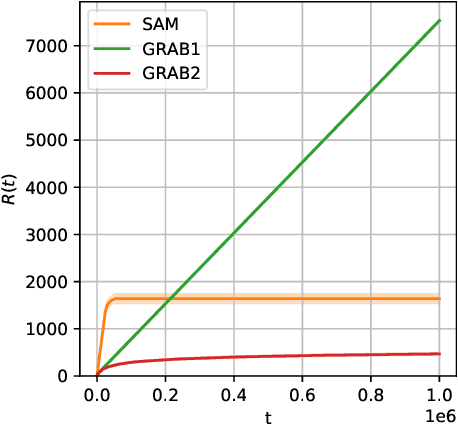
We tackle a new emerging problem, which is finding an optimal monopartite matching in a weighted graph. The semi-bandit version, where a full matching is sampled at each iteration, has been addressed by \cite{ADMA}, creating an algorithm with an expected regret matching $O(\frac{L\log(L)}{\Delta}\log(T))$ with $2L$ players, $T$ iterations and a minimum reward gap $\Delta$. We reduce this bound in two steps. First, as in \cite{GRAB} and \cite{UniRank} we use the unimodality property of the expected reward on the appropriate graph to design an algorithm with a regret in $O(L\frac{1}{\Delta}\log(T))$. Secondly, we show that by moving the focus towards the main question `\emph{Is user $i$ better than user $j$?}' this regret becomes $O(L\frac{\Delta}{\tilde{\Delta}^2}\log(T))$, where $\Tilde{\Delta} > \Delta$ derives from a better way of comparing users. Some experimental results finally show these theoretical results are corroborated in practice.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge