Understanding the Pathologies of Approximate Policy Evaluation when Combined with Greedification in Reinforcement Learning

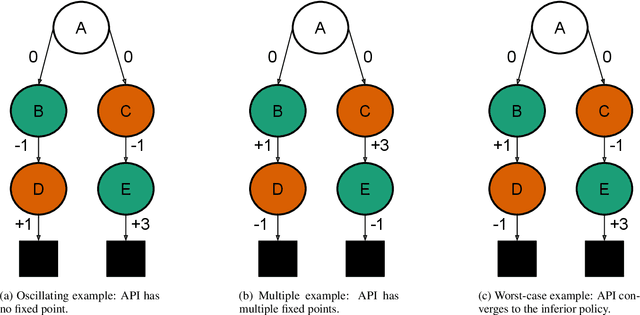
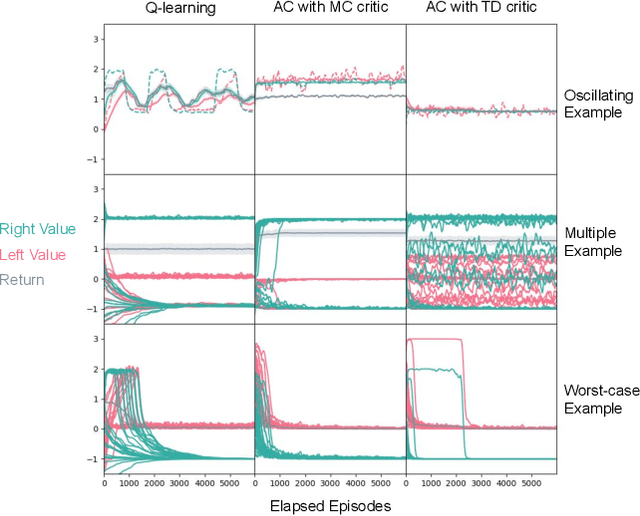
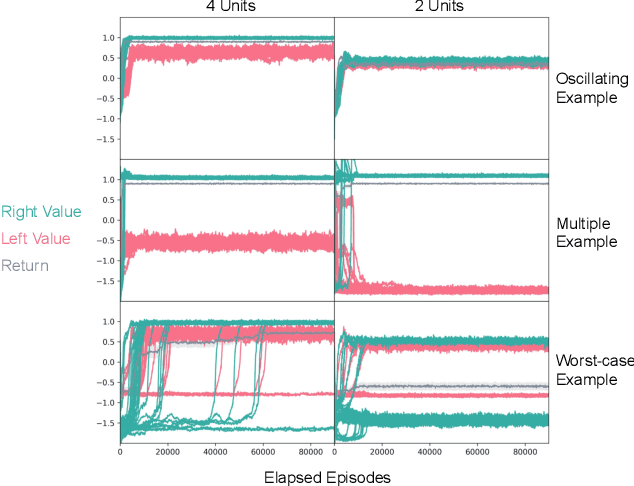
Despite empirical success, the theory of reinforcement learning (RL) with value function approximation remains fundamentally incomplete. Prior work has identified a variety of pathological behaviours that arise in RL algorithms that combine approximate on-policy evaluation and greedification. One prominent example is policy oscillation, wherein an algorithm may cycle indefinitely between policies, rather than converging to a fixed point. What is not well understood however is the quality of the policies in the region of oscillation. In this paper we present simple examples illustrating that in addition to policy oscillation and multiple fixed points -- the same basic issue can lead to convergence to the worst possible policy for a given approximation. Such behaviours can arise when algorithms optimize evaluation accuracy weighted by the distribution of states that occur under the current policy, but greedify based on the value of states which are rare or nonexistent under this distribution. This means the values used for greedification are unreliable and can steer the policy in undesirable directions. Our observation that this can lead to the worst possible policy shows that in a general sense such algorithms are unreliable. The existence of such examples helps to narrow the kind of theoretical guarantees that are possible and the kind of algorithmic ideas that are likely to be helpful. We demonstrate analytically and experimentally that such pathological behaviours can impact a wide range of RL and dynamic programming algorithms; such behaviours can arise both with and without bootstrapping, and with linear function approximation as well as with more complex parameterized functions like neural networks.