Understanding Regularization to Visualize Convolutional Neural Networks
Paper and Code
Apr 20, 2018
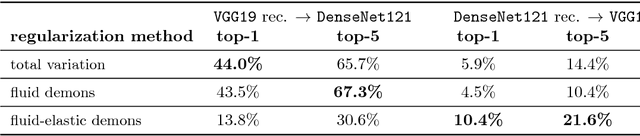

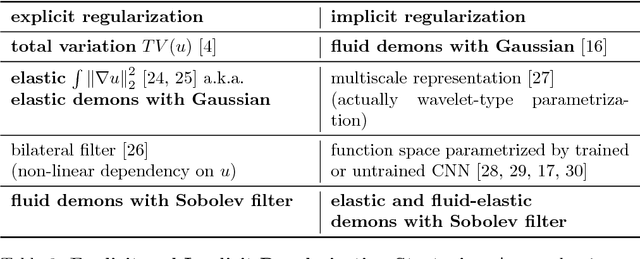
Variational methods for revealing visual concepts learned by convolutional neural networks have gained significant attention during the last years. Being based on noisy gradients obtained via back-propagation such methods require the application of regularization strategies. We present a mathematical framework unifying previously employed regularization methods. Within this framework, we propose a novel technique based on Sobolev gradients which can be implemented via convolutions and does not require specialized numerical treatment, such as total variation regularization. The experiments performed on feature inversion and activation maximization demonstrate the benefit of a unified approach to regularization, such as sharper reconstructions via the proposed Sobolev filters and a better control over reconstructed scales.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge