Understanding Decoupled and Early Weight Decay
Paper and Code
Dec 27, 2020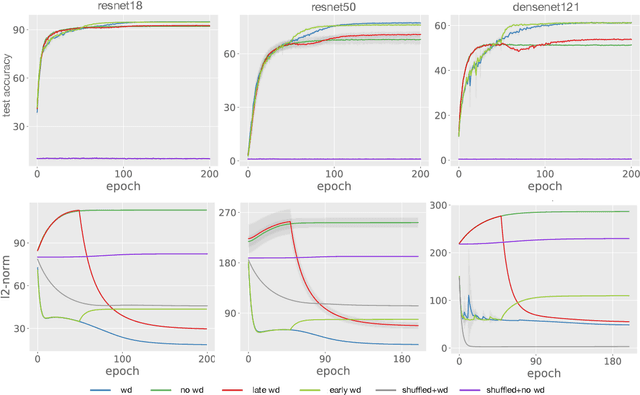
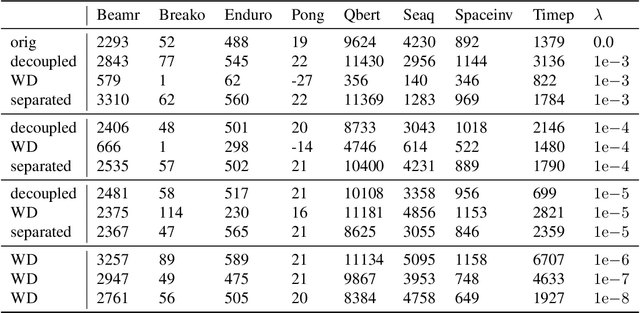
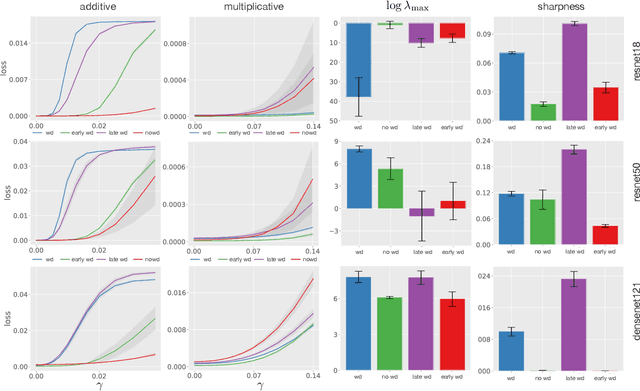
Weight decay (WD) is a traditional regularization technique in deep learning, but despite its ubiquity, its behavior is still an area of active research. Golatkar et al. have recently shown that WD only matters at the start of the training in computer vision, upending traditional wisdom. Loshchilov et al. show that for adaptive optimizers, manually decaying weights can outperform adding an $l_2$ penalty to the loss. This technique has become increasingly popular and is referred to as decoupled WD. The goal of this paper is to investigate these two recent empirical observations. We demonstrate that by applying WD only at the start, the network norm stays small throughout training. This has a regularizing effect as the effective gradient updates become larger. However, traditional generalizations metrics fail to capture this effect of WD, and we show how a simple scale-invariant metric can. We also show how the growth of network weights is heavily influenced by the dataset and its generalization properties. For decoupled WD, we perform experiments in NLP and RL where adaptive optimizers are the norm. We demonstrate that the primary issue that decoupled WD alleviates is the mixing of gradients from the objective function and the $l_2$ penalty in the buffers of Adam (which stores the estimates of the first-order moment). Adaptivity itself is not problematic and decoupled WD ensures that the gradients from the $l_2$ term cannot "drown out" the true objective, facilitating easier hyperparameter tuning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge