Understand Functionality and Dimensionality of Vector Embeddings: the Distributional Hypothesis, the Pairwise Inner Product Loss and Its Bias-Variance Trade-off

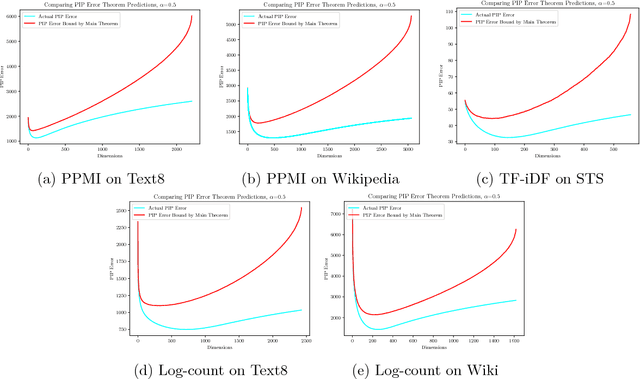
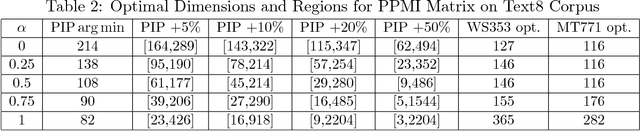
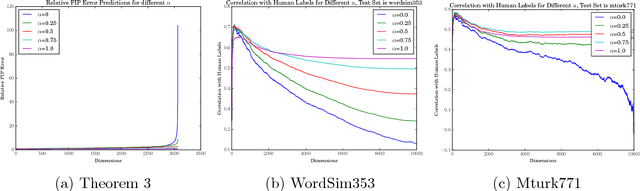
Vector embedding is a foundational building block of many deep learning models, especially in natural language processing. In this paper, we present a theoretical framework for understanding the effect of dimensionality on vector embeddings. We observe that the distributional hypothesis, a governing principle of statistical semantics, requires a natural unitary-invariance for vector embeddings. Motivated by the unitary-invariance observation, we propose the Pairwise Inner Product (PIP) loss, a unitary-invariant metric on the similarity between two embeddings. We demonstrate that the PIP loss captures the difference in functionality between embeddings, and that the PIP loss is tightly connect with two basic properties of vector embeddings, namely similarity and compositionality. By formulating the embedding training process as matrix factorization with noise, we reveal a fundamental bias-variance trade-off between the signal spectrum and noise power in the dimensionality selection process. This bias-variance trade-off sheds light on many empirical observations which have not been thoroughly explained, for example the existence of an optimal dimensionality. Moreover, we discover two new results about vector embeddings, namely their robustness against over-parametrization and their forward stability. The bias-variance trade-off of the PIP loss explicitly answers the fundamental open problem of dimensionality selection for vector embeddings.