Uncertainty Quantification in Deep Residual Neural Networks
Paper and Code
Jul 09, 2020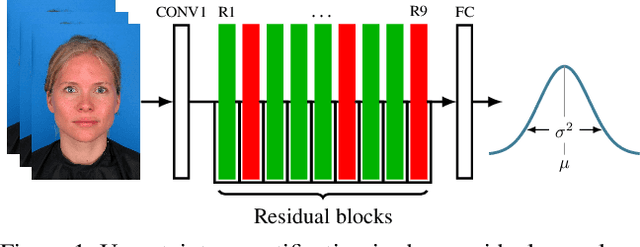
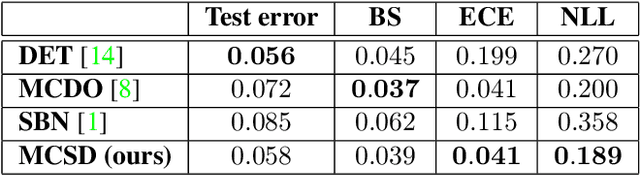


Uncertainty quantification is an important and challenging problem in deep learning. Previous methods rely on dropout layers which are not present in modern deep architectures or batch normalization which is sensitive to batch sizes. In this work, we address the problem of uncertainty quantification in deep residual networks by using a regularization technique called stochastic depth. We show that training residual networks using stochastic depth can be interpreted as a variational approximation to the intractable posterior over the weights in Bayesian neural networks. We demonstrate that by sampling from a distribution of residual networks with varying depth and shared weights, meaningful uncertainty estimates can be obtained. Moreover, compared to the original formulation of residual networks, our method produces well-calibrated softmax probabilities with only minor changes to the network's structure. We evaluate our approach on popular computer vision datasets and measure the quality of uncertainty estimates. We also test the robustness to domain shift and show that our method is able to express higher predictive uncertainty on out-of-distribution samples. Finally, we demonstrate how the proposed approach could be used to obtain uncertainty estimates in facial verification applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge