Ultrametric Component Analysis with Application to Analysis of Text and of Emotion
Paper and Code
Sep 14, 2013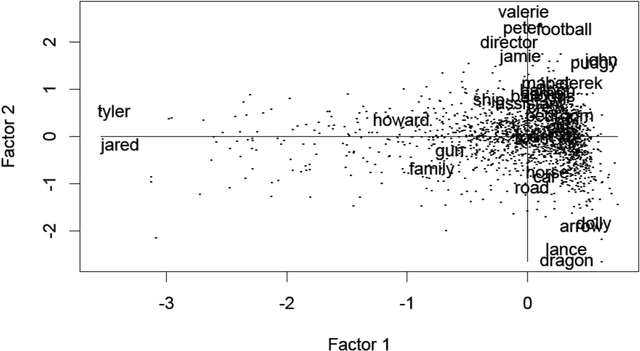
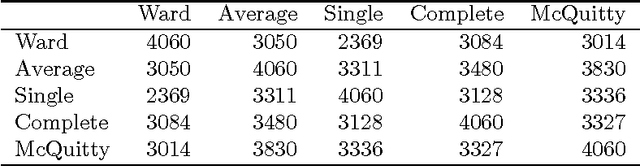
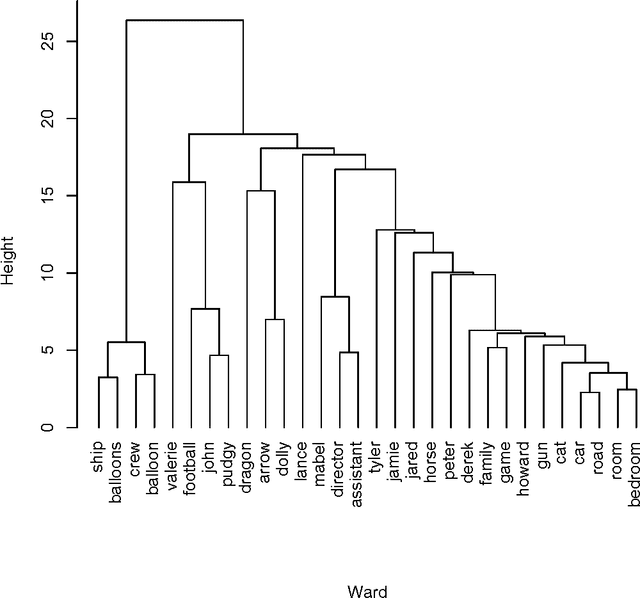
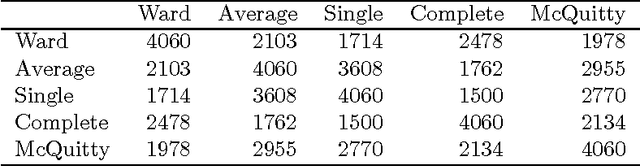
We review the theory and practice of determining what parts of a data set are ultrametric. It is assumed that the data set, to begin with, is endowed with a metric, and we include discussion of how this can be brought about if a dissimilarity, only, holds. The basis for part of the metric-endowed data set being ultrametric is to consider triplets of the observables (vectors). We develop a novel consensus of hierarchical clusterings. We do this in order to have a framework (including visualization and supporting interpretation) for the parts of the data that are determined to be ultrametric. Furthermore a major objective is to determine locally ultrametric relationships as opposed to non-local ultrametric relationships. As part of this work, we also study a particular property of our ultrametricity coefficient, namely, it being a function of the difference of angles of the base angles of the isosceles triangle. This work is completed by a review of related work, on consensus hierarchies, and of a major new application, namely quantifying and interpreting the emotional content of narrative.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge