Truncated Variational Sampling for "Black Box" Optimization of Generative Models
Paper and Code
Feb 22, 2018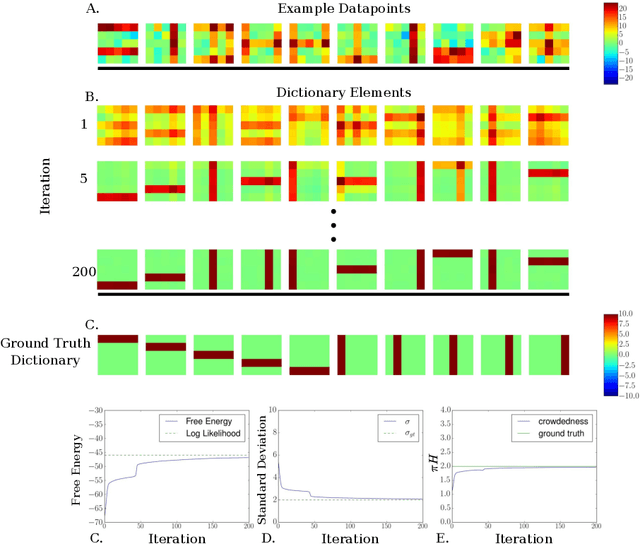
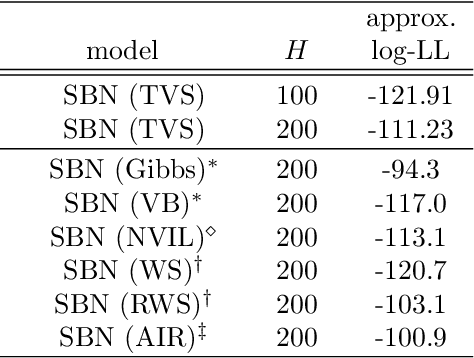
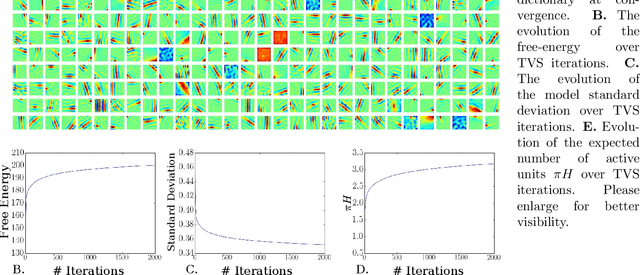
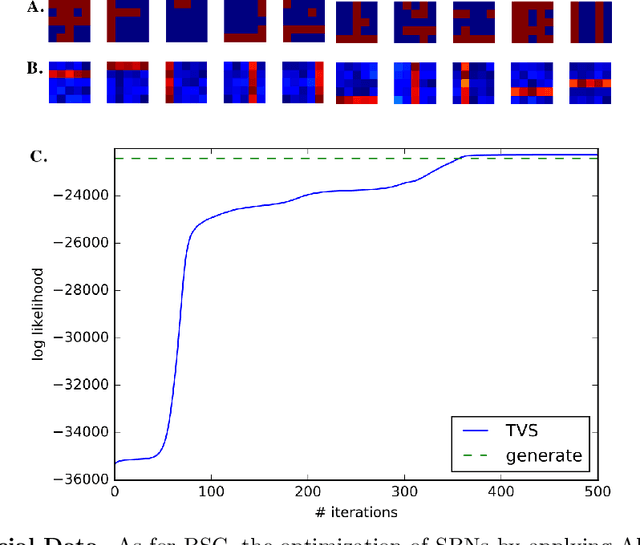
We investigate the optimization of two probabilistic generative models with binary latent variables using a novel variational EM approach. The approach distinguishes itself from previous variational approaches by using latent states as variational parameters. Here we use efficient and general purpose sampling procedures to vary the latent states, and investigate the "black box" applicability of the resulting optimization procedure. For general purpose applicability, samples are drawn from approximate marginal distributions of the considered generative model as well as from the model's prior distribution. As such, variational sampling is defined in a generic form, and is directly executable for a given model. As a proof of concept, we then apply the novel procedure (A) to Binary Sparse Coding (a model with continuous observables), and (B) to basic Sigmoid Belief Networks (which are models with binary observables). Numerical experiments verify that the investigated approach efficiently as well as effectively increases a variational free energy objective without requiring any additional analytical steps.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge