Tropical Polynomial Division and Neural Networks

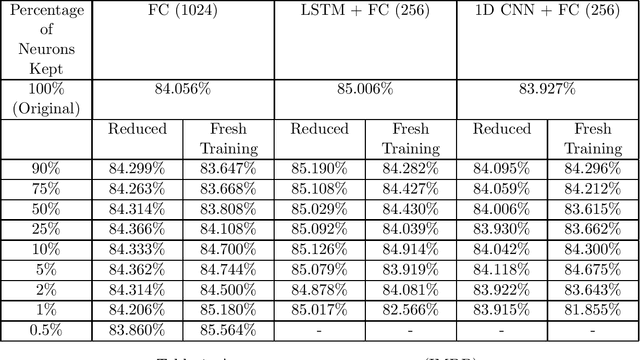
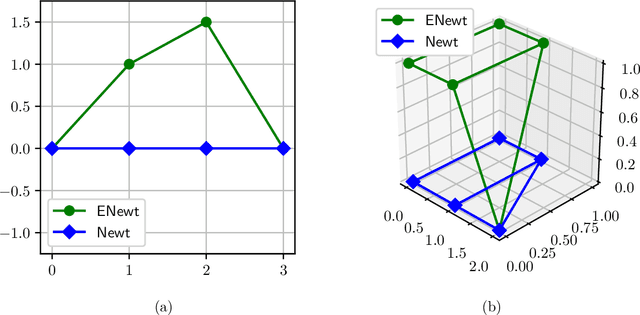
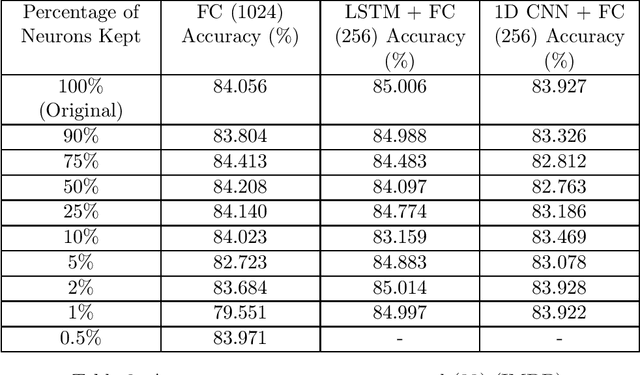
In this work, we examine the process of Tropical Polynomial Division, a geometric method which seeks to emulate the division of regular polynomials, when applied to those of the max-plus semiring. This is done via the approximation of the Newton Polytope of the dividend polynomial by that of the divisor. This process is afterwards generalized and applied in the context of neural networks with ReLU activations. In particular, we make use of the intuition it provides, in order to minimize a two-layer fully connected network, trained for a binary classification problem. This method is later evaluated on a variety of experiments, demonstrating its capability to approximate a network, with minimal loss in performance.