Transforming RIS-Assisted Passive Beamforming from Tedious to Simple: A Relaxation Algorithm for Rician Channel
Paper and Code
Nov 22, 2022

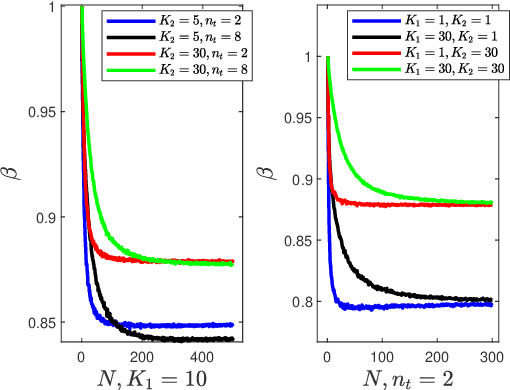
This paper investigates the problem of maximizing the signal-to-noise ratio (SNR) in reconfigurable intelligent surface (RIS)-assisted MISO communication systems. The problem will be reformulated as a complex quadratic form problem with unit circle constraints. We proved that the SNR maximizing problem has a closed-form global optimal solution when it is a rank-one problem, whereas the former researchers regarded it as an optimization problem. Moreover, We propose a relaxation algorithm (RA) that relaxes the constraints to that of Rayleigh's quotient problem and then projects the solution back, where the SNR obtained by RA achieves much the same SNR as the upper bound but with significantly low time consumption. Then we asymptotically analyze its performance when the transmitter antennas n_t and the number of units of RIS N grow large together, with N/n_t -> c. Finally, our numerical simulations show that RA achieves over 98% of the performance of the upper bound and takes below 1% time consumption of manifold optimization (MO) and 0.1% of semidefinite relaxation (SDR).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge