Transformed $\ell_1$ Regularization for Learning Sparse Deep Neural Networks
Paper and Code
Jan 04, 2019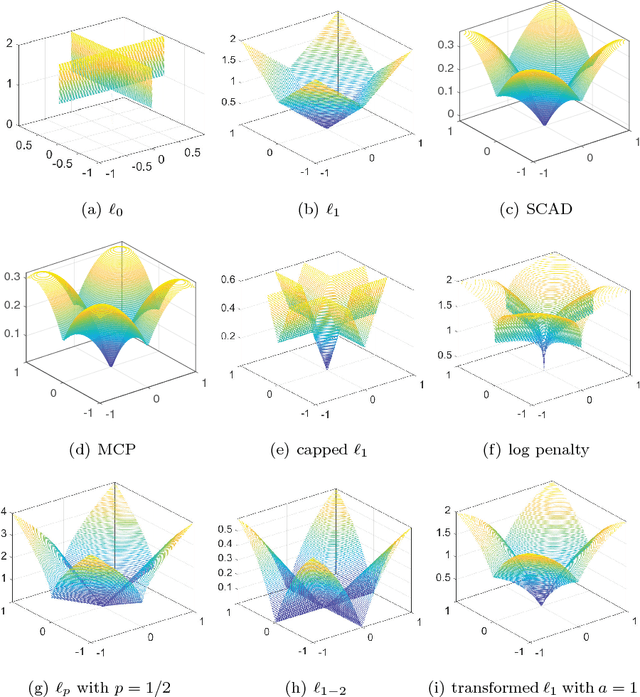

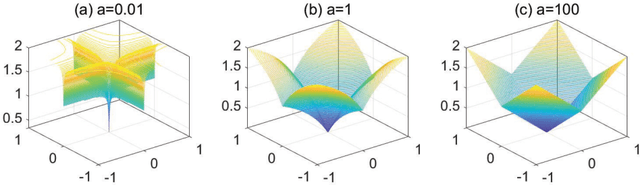
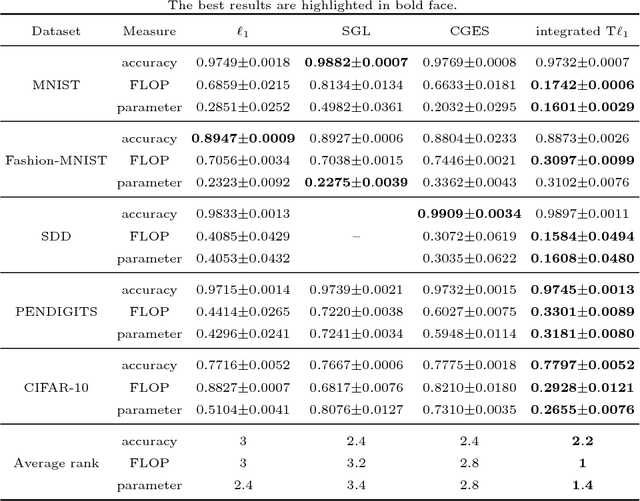
Deep neural networks (DNNs) have achieved extraordinary success in numerous areas. However, to attain this success, DNNs often carry a large number of weight parameters, leading to heavy costs of memory and computation resources. Overfitting is also likely to happen in such network when the training data are insufficient. These shortcomings severely hinder the application of DNNs in resource-constrained platforms. In fact, many network weights are known to be redundant and can be removed from the network without much loss of performance. To this end, we introduce a new non-convex integrated transformed $\ell_1$ regularizer to promote sparsity for DNNs, which removes both redundant connections and unnecessary neurons simultaneously. To be specific, we apply the transformed $\ell_1$ to the matrix space of network weights and utilize it to remove redundant connections. Besides, group sparsity is also employed as an auxiliary to remove unnecessary neurons. An efficient stochastic proximal gradient algorithm is presented to solve the new model at the same time. To the best of our knowledge, this is the first work to utilize a non-convex regularizer in sparse optimization based method to promote sparsity for DNNs. Experiments on several public datasets demonstrate the effectiveness of the proposed method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge