Trajectory Normalized Gradients for Distributed Optimization
Paper and Code
Jan 24, 2019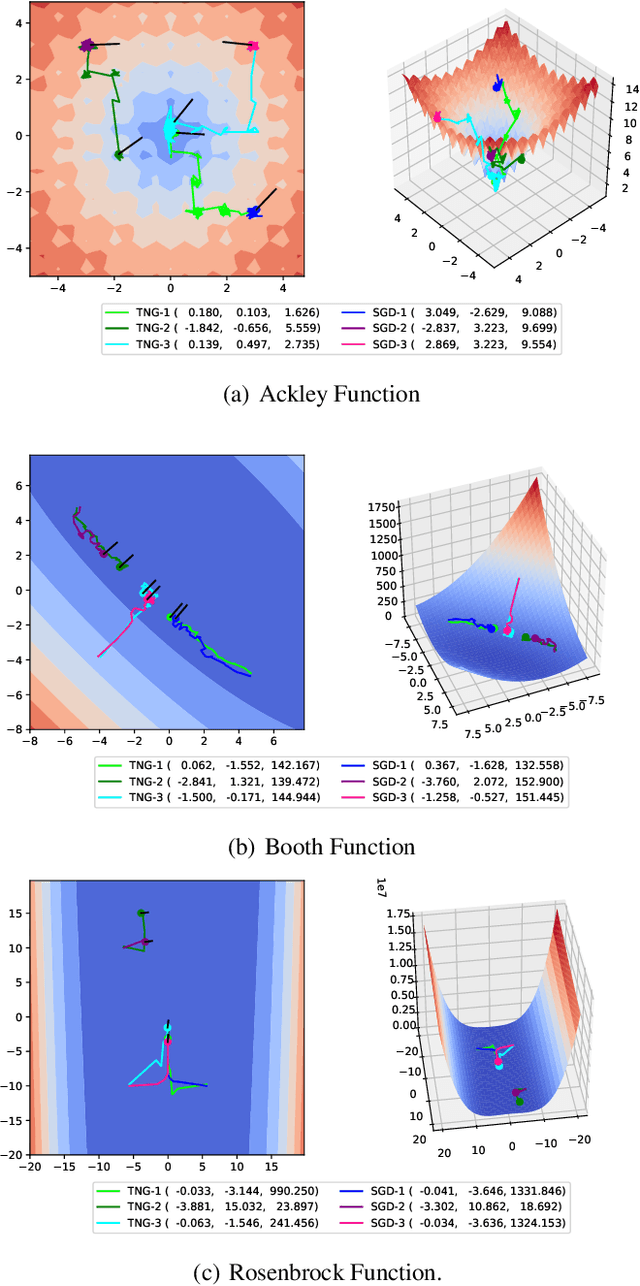
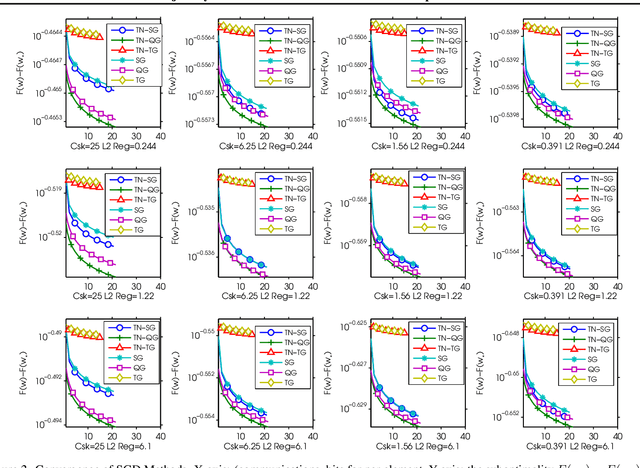
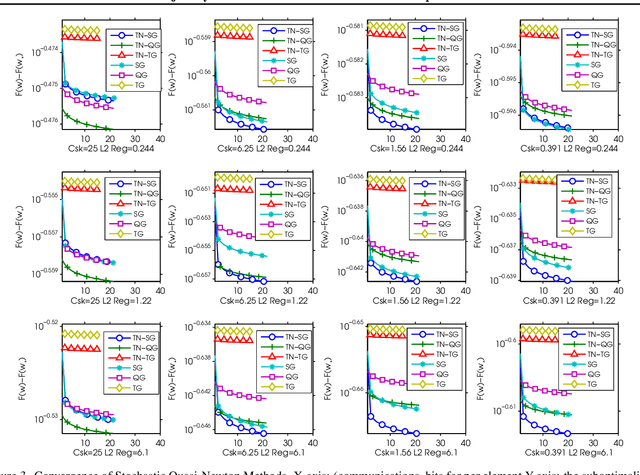
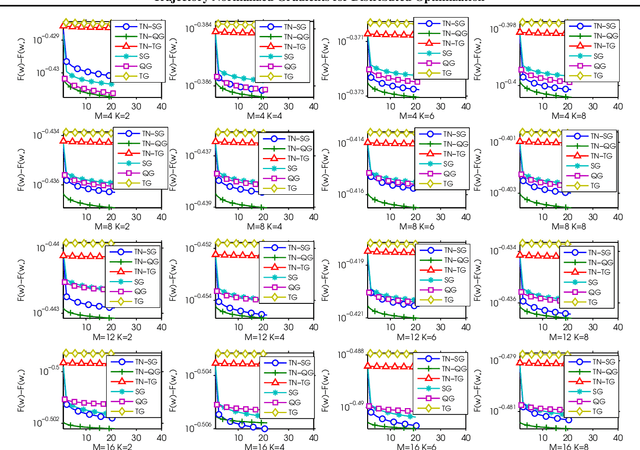
Recently, researchers proposed various low-precision gradient compression, for efficient communication in large-scale distributed optimization. Based on these work, we try to reduce the communication complexity from a new direction. We pursue an ideal bijective mapping between two spaces of gradient distribution, so that the mapped gradient carries greater information entropy after the compression. In our setting, all servers should share a reference gradient in advance, and they communicate via the normalized gradients, which are the subtraction or quotient, between current gradients and the reference. To obtain a reference vector that yields a stronger signal-to-noise ratio, dynamically in each iteration, we extract and fuse information from the past trajectory in hindsight, and search for an optimal reference for compression. We name this to be the trajectory-based normalized gradients (TNG). It bridges the research from different societies, like coding, optimization, systems, and learning. It is easy to implement and can universally combine with existing algorithms. Our experiments on benchmarking hard non-convex functions, convex problems like logistic regression demonstrate that TNG is more compression-efficient for communication of distributed optimization of general functions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge