Training Thinner and Deeper Neural Networks: Jumpstart Regularization
Paper and Code
Jan 30, 2022
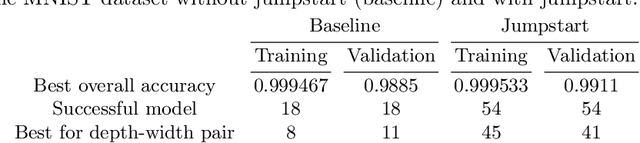
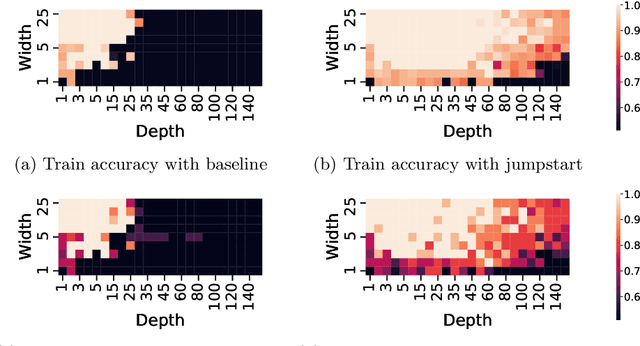
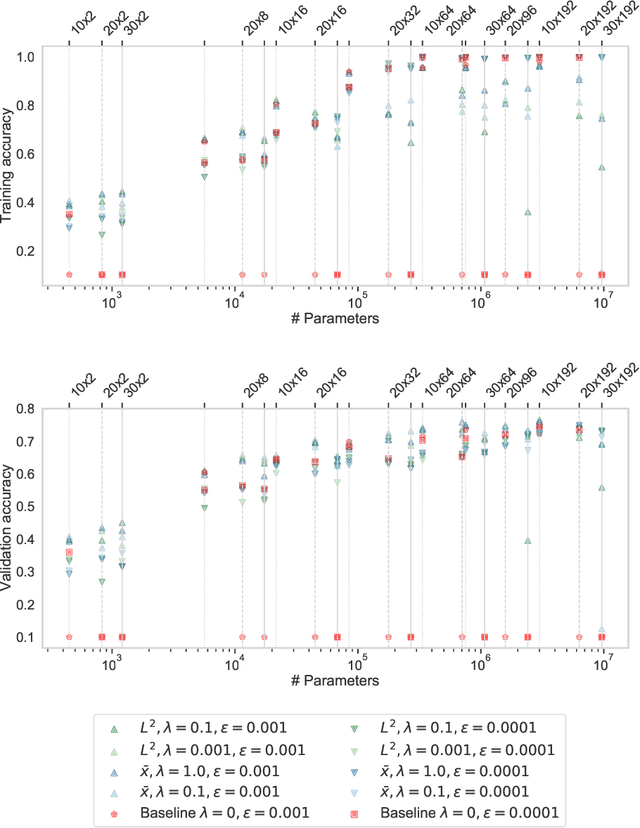
Neural networks are more expressive when they have multiple layers. In turn, conventional training methods are only successful if the depth does not lead to numerical issues such as exploding or vanishing gradients, which occur less frequently when the layers are sufficiently wide. However, increasing width to attain greater depth entails the use of heavier computational resources and leads to overparameterized models. These subsequent issues have been partially addressed by model compression methods such as quantization and pruning, some of which relying on normalization-based regularization of the loss function to make the effect of most parameters negligible. In this work, we propose instead to use regularization for preventing neurons from dying or becoming linear, a technique which we denote as jumpstart regularization. In comparison to conventional training, we obtain neural networks that are thinner, deeper, and - most importantly - more parameter-efficient.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge