Towards Unifying Logical Entailment and Statistical Estimation
Paper and Code
Feb 27, 2022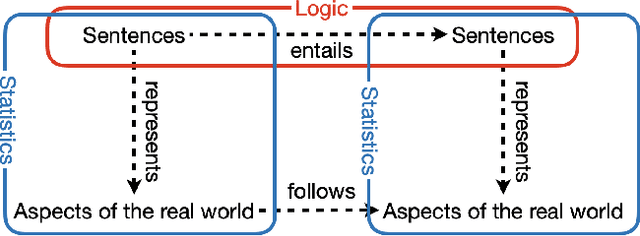
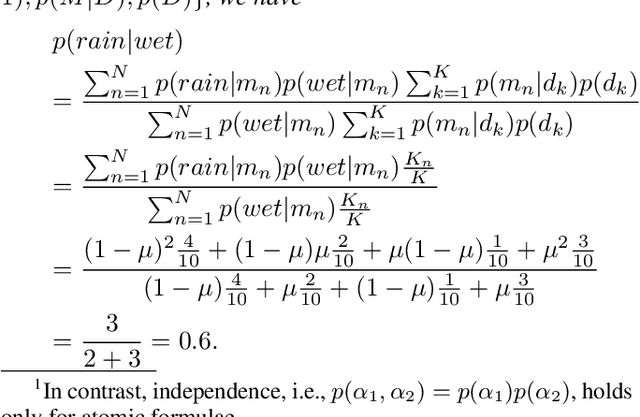
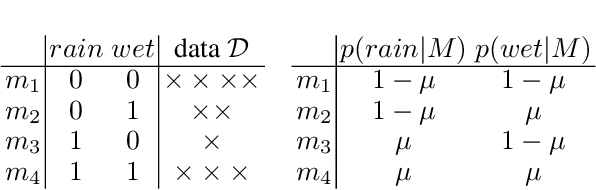

This paper gives a generative model of the interpretation of formal logic for data-driven logical reasoning. The key idea is to represent the interpretation as likelihood of a formula being true given a model of formal logic. Using the likelihood, Bayes' theorem gives the posterior of the model being the case given the formula. The posterior represents an inverse interpretation of formal logic that seeks models making the formula true. The likelihood and posterior cause Bayesian learning that gives the probability of the conclusion being true in the models where all the premises are true. This paper looks at statistical and logical properties of the Bayesian learning. It is shown that the generative model is a unified theory of several different types of reasoning in logic and statistics.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge