Towards Mixed-Precision Quantization of Neural Networks via Constrained Optimization
Paper and Code
Oct 13, 2021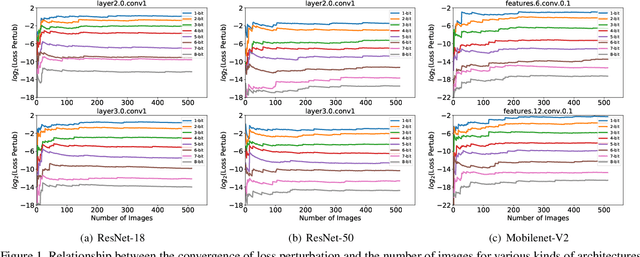
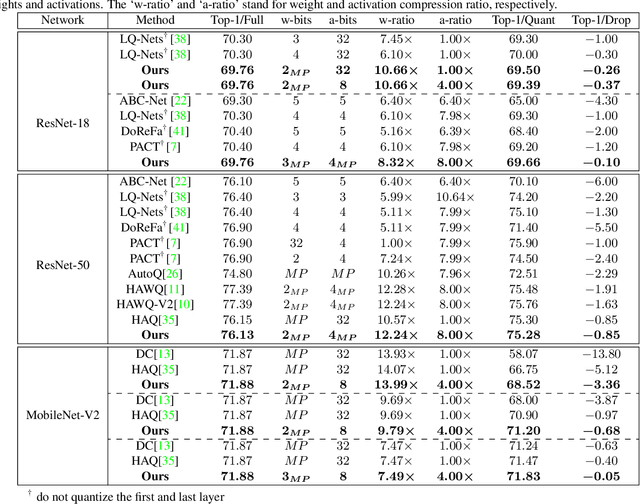
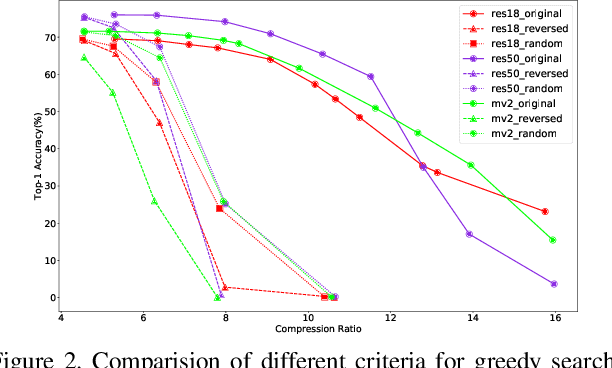
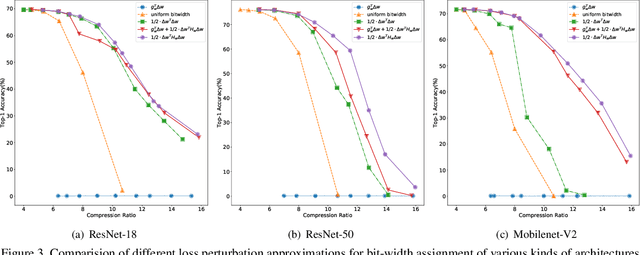
Quantization is a widely used technique to compress and accelerate deep neural networks. However, conventional quantization methods use the same bit-width for all (or most of) the layers, which often suffer significant accuracy degradation in the ultra-low precision regime and ignore the fact that emergent hardware accelerators begin to support mixed-precision computation. Consequently, we present a novel and principled framework to solve the mixed-precision quantization problem in this paper. Briefly speaking, we first formulate the mixed-precision quantization as a discrete constrained optimization problem. Then, to make the optimization tractable, we approximate the objective function with second-order Taylor expansion and propose an efficient approach to compute its Hessian matrix. Finally, based on the above simplification, we show that the original problem can be reformulated as a Multiple-Choice Knapsack Problem (MCKP) and propose a greedy search algorithm to solve it efficiently. Compared with existing mixed-precision quantization works, our method is derived in a principled way and much more computationally efficient. Moreover, extensive experiments conducted on the ImageNet dataset and various kinds of network architectures also demonstrate its superiority over existing uniform and mixed-precision quantization approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge