Towards a Spectrum of Graph Convolutional Networks
Paper and Code
May 04, 2018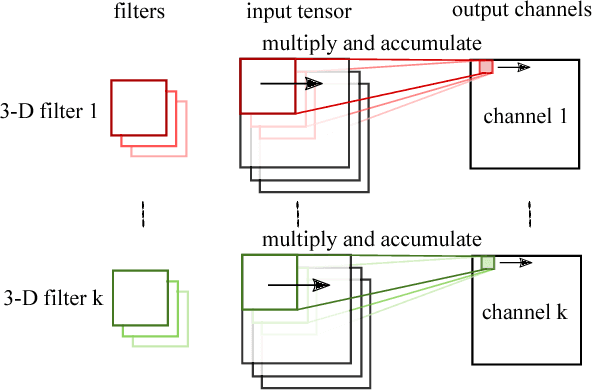
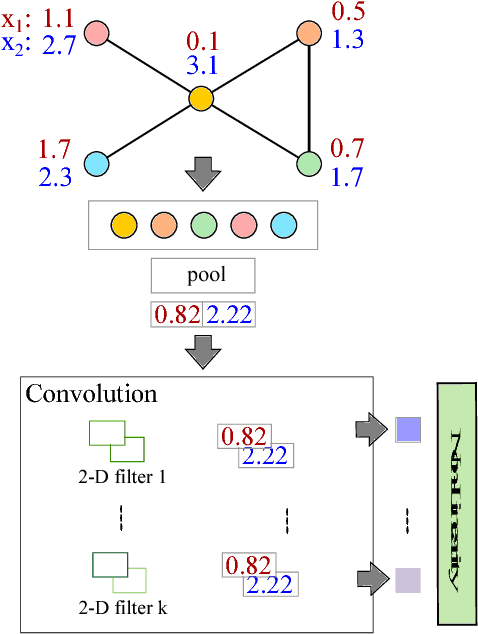
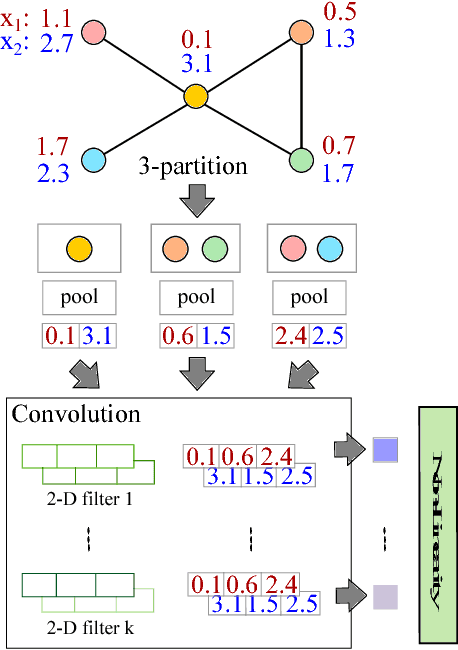
We present our ongoing work on understanding the limitations of graph convolutional networks (GCNs) as well as our work on generalizations of graph convolutions for representing more complex node attribute dependencies. Based on an analysis of GCNs with the help of the corresponding computation graphs, we propose a generalization of existing GCNs where the aggregation operations are (a) determined by structural properties of the local neighborhood graphs and (b) not restricted to weighted averages. We show that the proposed approach is strictly more expressive while requiring only a modest increase in the number of parameters and computations. We also show that the proposed generalization is identical to standard convolutional layers when applied to regular grid graphs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge