Times series averaging from a probabilistic interpretation of time-elastic kernel

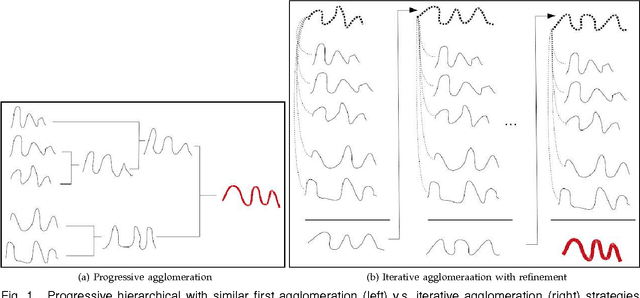
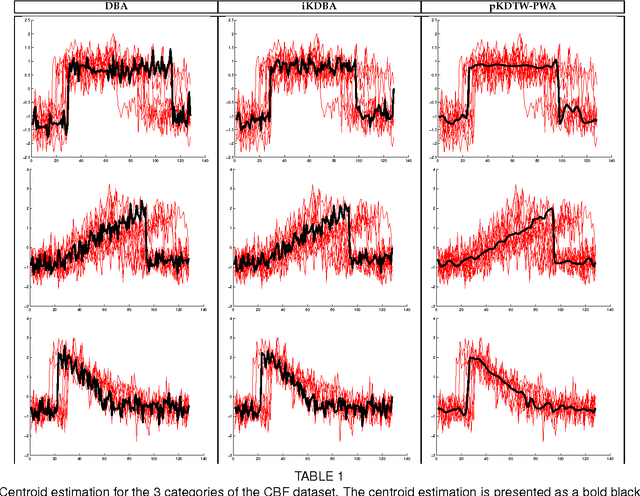
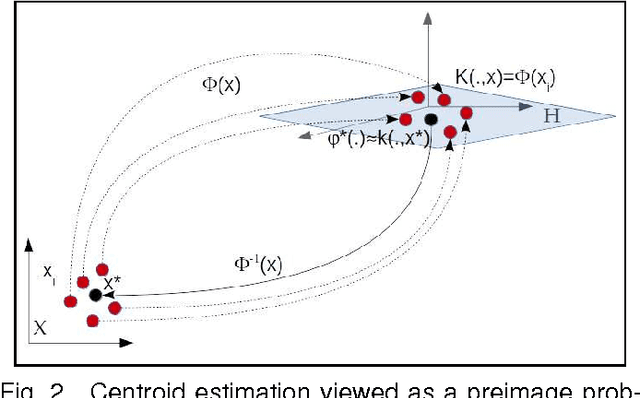
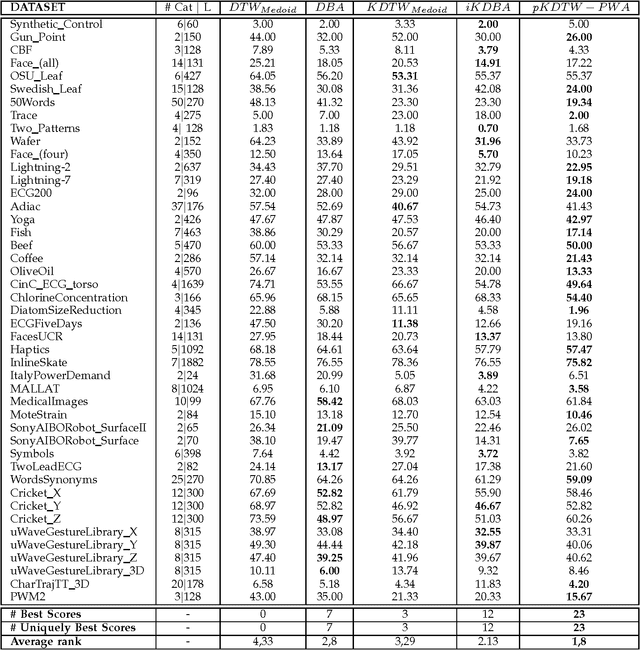
At the light of regularized dynamic time warping kernels, this paper reconsider the concept of time elastic centroid (TEC) for a set of time series. From this perspective, we show first how TEC can easily be addressed as a preimage problem. Unfortunately this preimage problem is ill-posed, may suffer from over-fitting especially for long time series and getting a sub-optimal solution involves heavy computational costs. We then derive two new algorithms based on a probabilistic interpretation of kernel alignment matrices that expresses in terms of probabilistic distributions over sets of alignment paths. The first algorithm is an iterative agglomerative heuristics inspired from the state of the art DTW barycenter averaging (DBA) algorithm proposed specifically for the Dynamic Time Warping measure. The second proposed algorithm achieves a classical averaging of the aligned samples but also implements an averaging of the time of occurrences of the aligned samples. It exploits a straightforward progressive agglomerative heuristics. An experimentation that compares for 45 time series datasets classification error rates obtained by first near neighbors classifiers exploiting a single medoid or centroid estimate to represent each categories show that: i) centroids based approaches significantly outperform medoids based approaches, ii) on the considered experience, the two proposed algorithms outperform the state of the art DBA algorithm, and iii) the second proposed algorithm that implements an averaging jointly in the sample space and along the time axes emerges as the most significantly robust time elastic averaging heuristic with an interesting noise reduction capability. Index Terms-Time series averaging Time elastic kernel Dynamic Time Warping Time series clustering and classification.