Time Discretization-Invariant Safe Action Repetition for Policy Gradient Methods
Paper and Code
Dec 01, 2021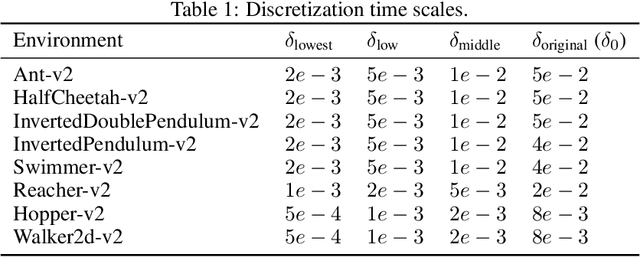

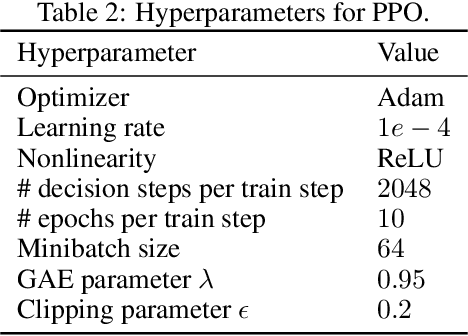

In reinforcement learning, continuous time is often discretized by a time scale $\delta$, to which the resulting performance is known to be highly sensitive. In this work, we seek to find a $\delta$-invariant algorithm for policy gradient (PG) methods, which performs well regardless of the value of $\delta$. We first identify the underlying reasons that cause PG methods to fail as $\delta \to 0$, proving that the variance of the PG estimator can diverge to infinity in stochastic environments under a certain assumption of stochasticity. While durative actions or action repetition can be employed to have $\delta$-invariance, previous action repetition methods cannot immediately react to unexpected situations in stochastic environments. We thus propose a novel $\delta$-invariant method named Safe Action Repetition (SAR) applicable to any existing PG algorithm. SAR can handle the stochasticity of environments by adaptively reacting to changes in states during action repetition. We empirically show that our method is not only $\delta$-invariant but also robust to stochasticity, outperforming previous $\delta$-invariant approaches on eight MuJoCo environments with both deterministic and stochastic settings. Our code is available at https://vision.snu.ac.kr/projects/sar.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge