Tight Bounds on Low-degree Spectral Concentration of Submodular and XOS functions
Paper and Code
Aug 02, 2015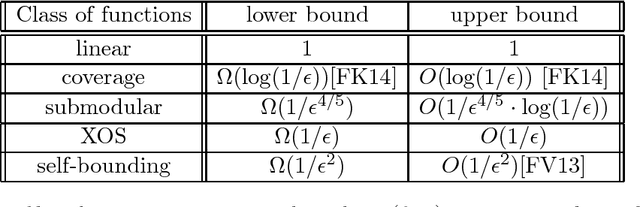
Submodular and fractionally subadditive (or equivalently XOS) functions play a fundamental role in combinatorial optimization, algorithmic game theory and machine learning. Motivated by learnability of these classes of functions from random examples, we consider the question of how well such functions can be approximated by low-degree polynomials in $\ell_2$ norm over the uniform distribution. This question is equivalent to understanding of the concentration of Fourier weight on low-degree coefficients, a central concept in Fourier analysis. We show that 1. For any submodular function $f:\{0,1\}^n \rightarrow [0,1]$, there is a polynomial of degree $O(\log (1/\epsilon) / \epsilon^{4/5})$ approximating $f$ within $\epsilon$ in $\ell_2$, and there is a submodular function that requires degree $\Omega(1/\epsilon^{4/5})$. 2. For any XOS function $f:\{0,1\}^n \rightarrow [0,1]$, there is a polynomial of degree $O(1/\epsilon)$ and there exists an XOS function that requires degree $\Omega(1/\epsilon)$. This improves on previous approaches that all showed an upper bound of $O(1/\epsilon^2)$ for submodular and XOS functions. The best previous lower bound was $\Omega(1/\epsilon^{2/3})$ for monotone submodular functions. Our techniques reveal new structural properties of submodular and XOS functions and the upper bounds lead to nearly optimal PAC learning algorithms for these classes of functions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge