Thwarting finite difference adversarial attacks with output randomization
Paper and Code
May 23, 2019

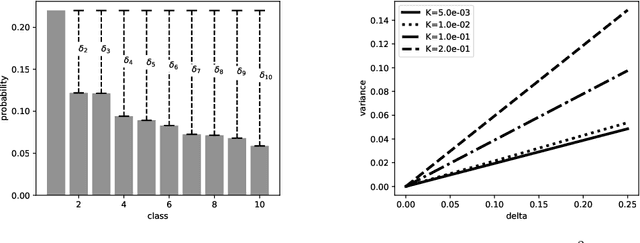
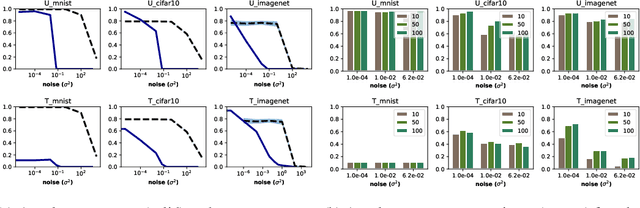
Adversarial examples pose a threat to deep neural network models in a variety of scenarios, from settings where the adversary has complete knowledge of the model and to the opposite "black box" setting. Black box attacks are particularly threatening as the adversary only needs access to the input and output of the model. Defending against black box adversarial example generation attacks is paramount as currently proposed defenses are not effective. Since these types of attacks rely on repeated queries to the model to estimate gradients over input dimensions, we investigate the use of randomization to thwart such adversaries from successfully creating adversarial examples. Randomization applied to the output of the deep neural network model has the potential to confuse potential attackers, however this introduces a tradeoff between accuracy and robustness. We show that for certain types of randomization, we can bound the probability of introducing errors by carefully setting distributional parameters. For the particular case of finite difference black box attacks, we quantify the error introduced by the defense in the finite difference estimate of the gradient. Lastly, we show empirically that the defense can thwart two adaptive black box adversarial attack algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge