Theory of Machine Learning Debugging via M-estimation

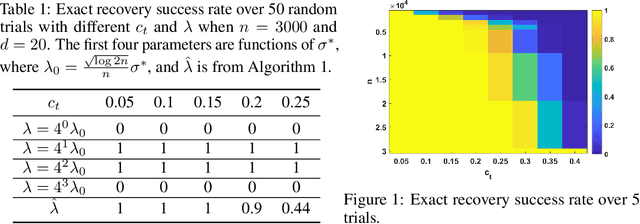
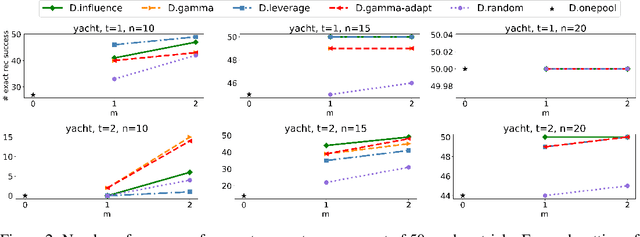
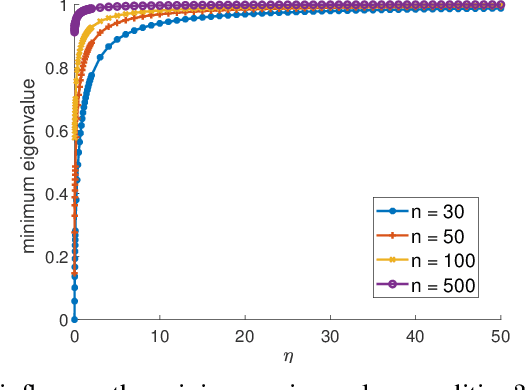
We investigate problems in penalized $M$-estimation, inspired by applications in machine learning debugging. Data are collected from two pools, one containing data with possibly contaminated labels, and the other which is known to contain only cleanly labeled points. We first formulate a general statistical algorithm for identifying buggy points and provide rigorous theoretical guarantees under the assumption that the data follow a linear model. We then present two case studies to illustrate the results of our general theory and the dependence of our estimator on clean versus buggy points. We further propose an algorithm for tuning parameter selection of our Lasso-based algorithm and provide corresponding theoretical guarantees. Finally, we consider a two-person "game" played between a bug generator and a debugger, where the debugger can augment the contaminated data set with cleanly labeled versions of points in the original data pool. We establish a theoretical result showing a sufficient condition under which the bug generator can always fool the debugger. Nonetheless, we provide empirical results showing that such a situation may not occur in practice, making it possible for natural augmentation strategies combined with our Lasso debugging algorithm to succeed.