Theoretical Analysis of Divide-and-Conquer ERM: Beyond Square Loss and RKHS
Paper and Code
Mar 17, 2020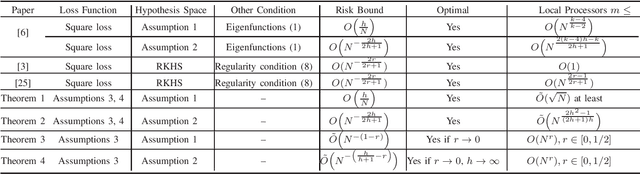
Theoretical analysis of the divide-and-conquer based distributed learning with least square loss in the reproducing kernel Hilbert space (RKHS) have recently been explored within the framework of learning theory. However, the studies on learning theory for general loss functions and hypothesis spaces remain limited. To fill the gap, we study the risk performance of distributed empirical risk minimization (ERM) for general loss functions and hypothesis spaces. The main contributions are two-fold. First, we derive two tight risk bounds under certain basic assumptions on the hypothesis space, as well as the smoothness, Lipschitz continuity, strong convexity of the loss function. Second, we further develop a more general risk bound for distributed ERM without the restriction of strong convexity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge