The whole and the parts: the MDL principle and the a-contrario framework

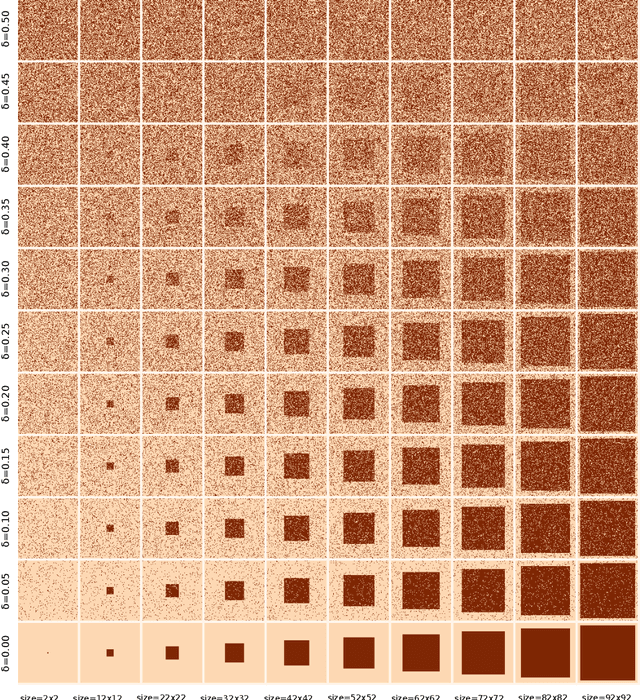
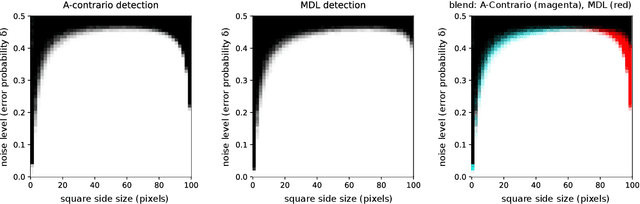
This work explores the connections between the Minimum Description Length (MDL) principle as developed by Rissanen, and the a-contrario framework for structure detection proposed by Desolneux, Moisan and Morel. The MDL principle focuses on the best interpretation for the whole data while the a-contrario approach concentrates on detecting parts of the data with anomalous statistics. Although framed in different theoretical formalisms, we show that both methodologies share many common concepts and tools in their machinery and yield very similar formulations in a number of interesting scenarios ranging from simple toy examples to practical applications such as polygonal approximation of curves and line segment detection in images. We also formulate the conditions under which both approaches are formally equivalent.