The Sketched Wasserstein Distance for mixture distributions
Paper and Code
Jun 26, 2022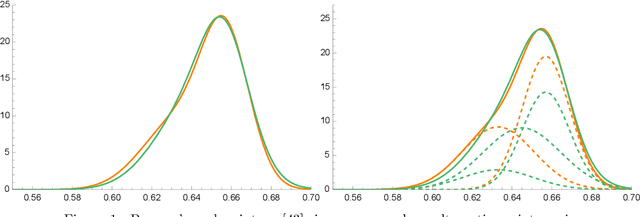

The Sketched Wasserstein Distance ($W^S$) is a new probability distance specifically tailored to finite mixture distributions. Given any metric $d$ defined on a set $\mathcal{A}$ of probability distributions, $W^S$ is defined to be the most discriminative convex extension of this metric to the space $\mathcal{S} = \textrm{conv}(\mathcal{A})$ of mixtures of elements of $\mathcal{A}$. Our representation theorem shows that the space $(\mathcal{S}, W^S)$ constructed in this way is isomorphic to a Wasserstein space over $\mathcal{X} = (\mathcal{A}, d)$. This result establishes a universality property for the Wasserstein distances, revealing them to be uniquely characterized by their discriminative power for finite mixtures. We exploit this representation theorem to propose an estimation methodology based on Kantorovich--Rubenstein duality, and prove a general theorem that shows that its estimation error can be bounded by the sum of the errors of estimating the mixture weights and the mixture components, for any estimators of these quantities. We derive sharp statistical properties for the estimated $W^S$ in the case of $p$-dimensional discrete $K$-mixtures, which we show can be estimated at a rate proportional to $\sqrt{K/N}$, up to logarithmic factors. We complement these bounds with a minimax lower bound on the risk of estimating the Wasserstein distance between distributions on a $K$-point metric space, which matches our upper bound up to logarithmic factors. This result is the first nearly tight minimax lower bound for estimating the Wasserstein distance between discrete distributions. Furthermore, we construct $\sqrt{N}$ asymptotically normal estimators of the mixture weights, and derive a $\sqrt{N}$ distributional limit of our estimator of $W^S$ as a consequence. Simulation studies and a data analysis provide strong support on the applicability of the new Sketched Wasserstein Distance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge