The Power of Constraint Grammars Revisited
Paper and Code
Jul 17, 2017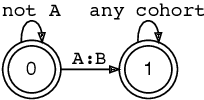
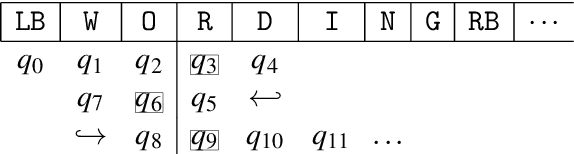
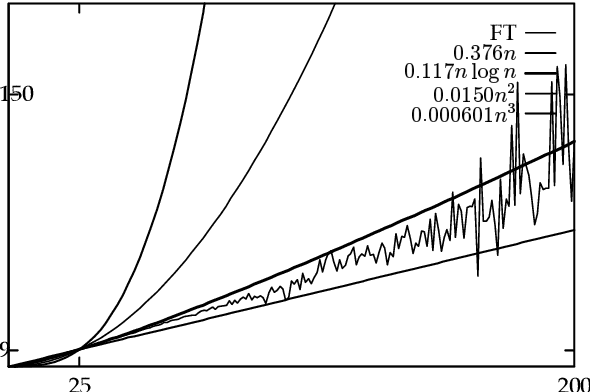
Sequential Constraint Grammar (SCG) (Karlsson, 1990) and its extensions have lacked clear connections to formal language theory. The purpose of this article is to lay a foundation for these connections by simplifying the definition of strings processed by the grammar and by showing that Nonmonotonic SCG is undecidable and that derivations similar to the Generative Phonology exist. The current investigations propose resource bounds that restrict the generative power of SCG to a subset of context sensitive languages and present a strong finite-state condition for grammars as wholes. We show that a grammar is equivalent to a finite-state transducer if it is implemented with a Turing machine that runs in o(n log n) time. This condition opens new finite-state hypotheses and avenues for deeper analysis of SCG instances in the way inspired by Finite-State Phonology.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge