The Missing Invariance Principle Found -- the Reciprocal Twin of Invariant Risk Minimization

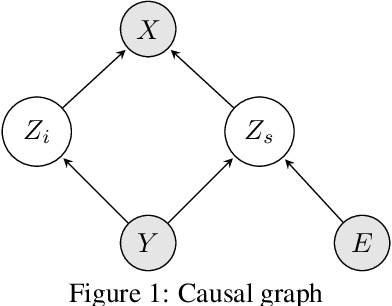
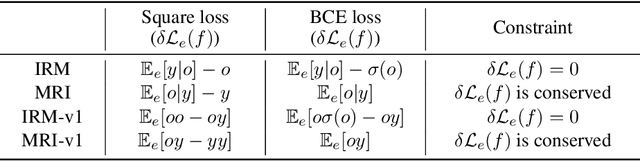
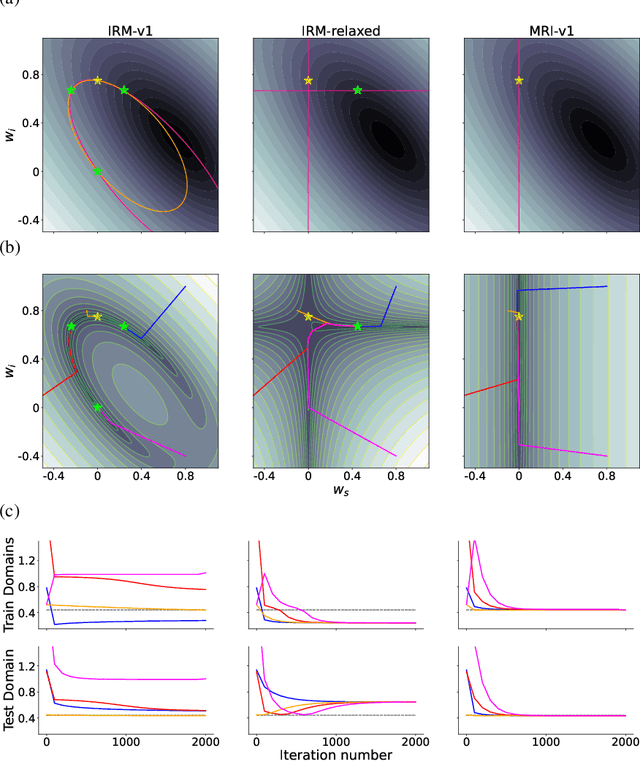
Machine learning models often generalize poorly to out-of-distribution (OOD) data as a result of relying on features that are spuriously correlated with the label during training. Recently, the technique of Invariant Risk Minimization (IRM) was proposed to learn predictors that only use invariant features by conserving the feature-conditioned class expectation $\mathbb{E}_e[y|f(x)]$ across environments. However, more recent studies have demonstrated that IRM can fail in various task settings. Here, we identify a fundamental flaw of IRM formulation that causes the failure. We then introduce a complementary notion of invariance, MRI, that is based on conserving the class-conditioned feature expectation $\mathbb{E}_e[f(x)|y]$ across environments, that corrects for the flaw in IRM. Further, we introduce a simplified, practical version of the MRI formulation called as MRI-v1. We note that this constraint is convex which confers it with an advantage over the practical version of IRM, IRM-v1, which imposes non-convex constraints. We prove that in a general linear problem setting, MRI-v1 can guarantee invariant predictors given sufficient environments. We also empirically demonstrate that MRI strongly out-performs IRM and consistently achieves near-optimal OOD generalization in image-based nonlinear problems.