The Logic for a Mildly Context-Sensitive Fragment of the Lambek-Grishin Calculus

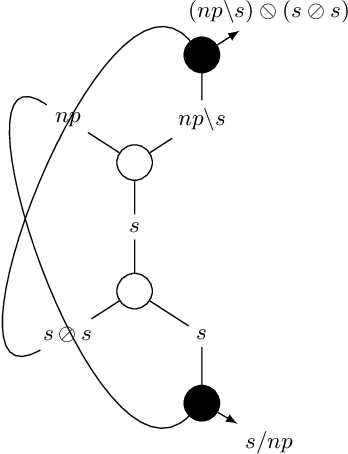
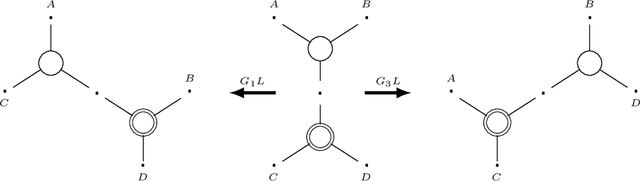
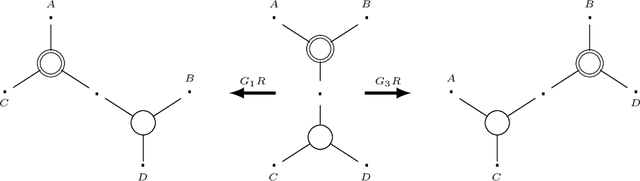
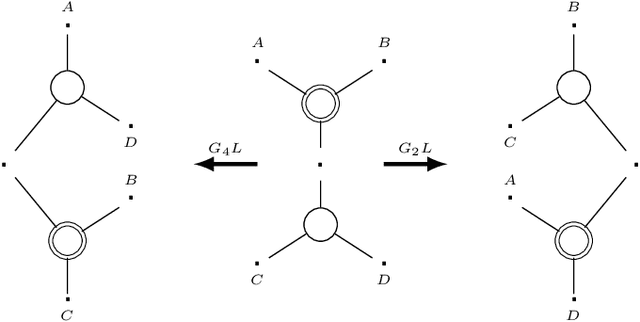
While context-free grammars are characterized by a simple proof-theoretic grammatical formalism namely categorial grammar and its logic the Lambek calculus, no such characterizations were known for tree-adjoining grammars, and even for any mildly context-sensitive languages classes in the last forty years despite some efforts. We settle this problem in this paper. On the basis of the existing fragment of the Lambek-Grishin calculus which captures tree-adjoining languages, we present a logic called HLG: a proof-theoretic characterization of tree-adjoining languages based on the Lambek-Grishin calculus restricted to Hyperedge-replacement grammar with rank two studied by Moot. HLG is defined in display calculus with cut-admissibility. Several new techniques are introduced for the proofs, such as purely structural connectives, usefulness, and a graph-theoretic argument on proof nets for HLG.