The GTR-model: a universal framework for quantum-like measurements
Paper and Code
Dec 02, 2015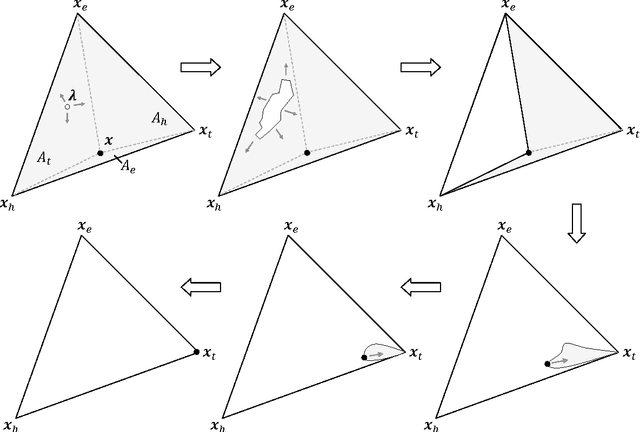
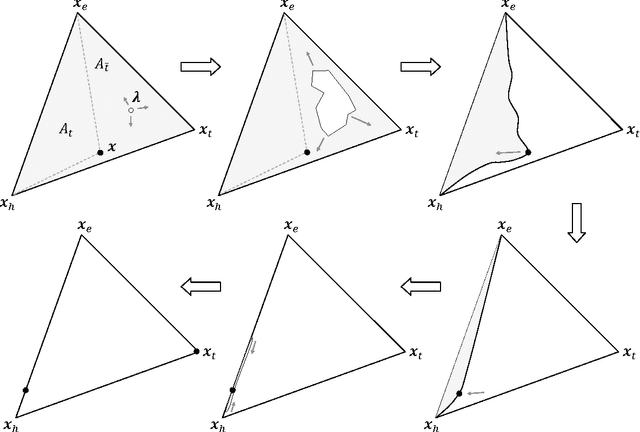
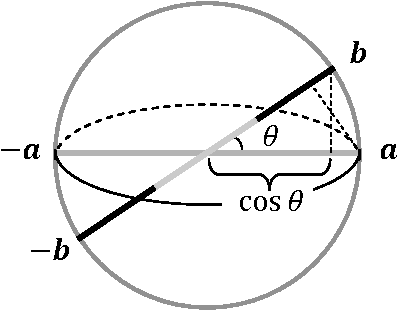
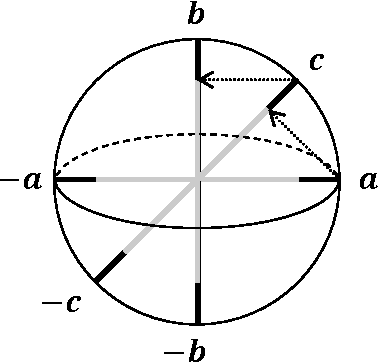
We present a very general geometrico-dynamical description of physical or more abstract entities, called the 'general tension-reduction' (GTR) model, where not only states, but also measurement-interactions can be represented, and the associated outcome probabilities calculated. Underlying the model is the hypothesis that indeterminism manifests as a consequence of unavoidable fluctuations in the experimental context, in accordance with the 'hidden-measurements interpretation' of quantum mechanics. When the structure of the state space is Hilbertian, and measurements are of the 'universal' kind, i.e., are the result of an average over all possible ways of selecting an outcome, the GTR-model provides the same predictions of the Born rule, and therefore provides a natural completed version of quantum mechanics. However, when the structure of the state space is non-Hilbertian and/or not all possible ways of selecting an outcome are available to be actualized, the predictions of the model generally differ from the quantum ones, especially when sequential measurements are considered. Some paradigmatic examples will be discussed, taken from physics and human cognition. Particular attention will be given to some known psychological effects, like question order effects and response replicability, which we show are able to generate non-Hilbertian statistics. We also suggest a realistic interpretation of the GTR-model, when applied to human cognition and decision, which we think could become the generally adopted interpretative framework in quantum cognition research.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge