The Explanation Game: Explaining Machine Learning Models with Cooperative Game Theory

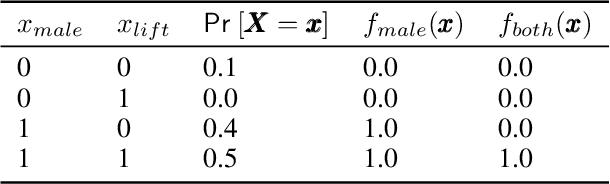
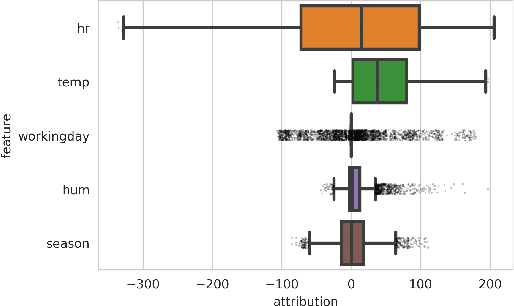
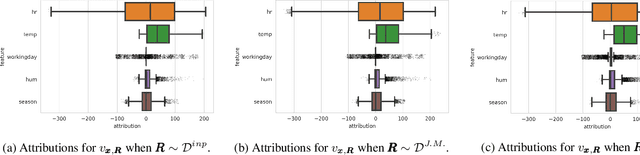
Recently, a number of techniques have been proposed to explain a machine learning (ML) model's prediction by attributing it to the corresponding input features. Popular among these are techniques that apply the Shapley value method from cooperative game theory. While existing papers focus on the axiomatic motivation of Shapley values, and efficient techniques for computing them, they do not justify the game formulations used. For instance, we find that the SHAP algorithm's formulation (Lundberg and Lee 2017) may give substantial attributions to features that play no role in a model. In this work, we study the game formulations underpinning several existing methods. Using a series of simple models, we illustrate how their subtle differences can yield large differences in attribution for the same prediction. We then present a general game formulation that unifies existing methods. After discussing the primitive of single-reference games, we decompose the Shapley values of the general game formulation into Shapley values of single-reference games. This is instructive in several ways. First, it enables confidence intervals on estimated attributions, which are not offered by previous works. Second, it enables different contrastive explanations of a prediction through comparison with different groups of reference inputs. We tie this idea to classic work on Norm Theory (Kahneman and Miller 1986) in cognitive psychology, and propose a general framework for generating explanations for ML models, called formulate, approximate, and explain (FAE). We apply this framework to explaining black-box models trained on two UCI datasets and a Lending Club dataset.