The estimation of training accuracy for two-layer neural networks on random datasets without training

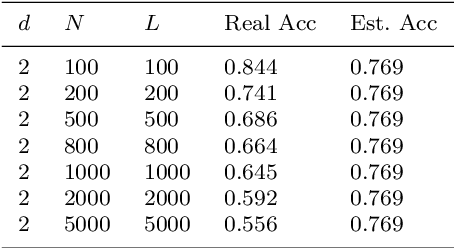
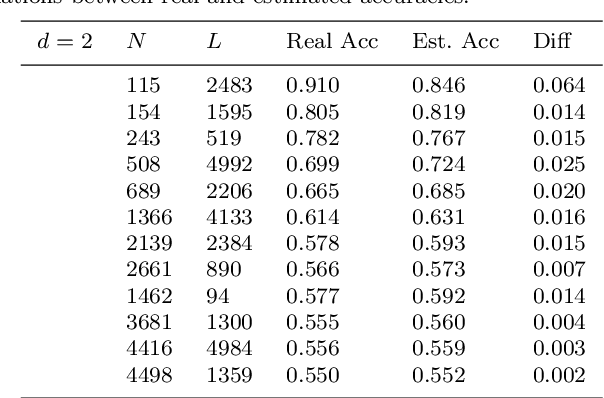
Although the neural network (NN) technique plays an important role in machine learning, understanding the mechanism of NN models and the transparency of deep learning still require more basic research. In this study we propose a novel theory based on space partitioning to estimate the approximate training accuracy for two-layer neural networks on random datasets without training. There appear to be no other studies that have proposed a method to estimate training accuracy without using input data or trained models. Our method estimates the training accuracy for two-layer fully-connected neural networks on two-class random datasets using only three arguments: the dimensionality of inputs (d), the number of inputs (N), and the number of neurons in the hidden layer (L). We have verified our method using real training accuracies in our experiments. The results indicate that the method will work for any dimension, and the proposed theory could extend also to estimate deeper NN models. This study may provide a starting point for a new way for researchers to make progress on the difficult problem of understanding deep learning.