The Effect of Prior Lipschitz Continuity on the Adversarial Robustness of Bayesian Neural Networks
Paper and Code
Jan 07, 2021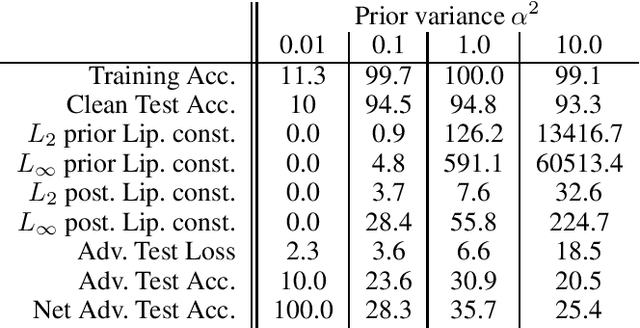
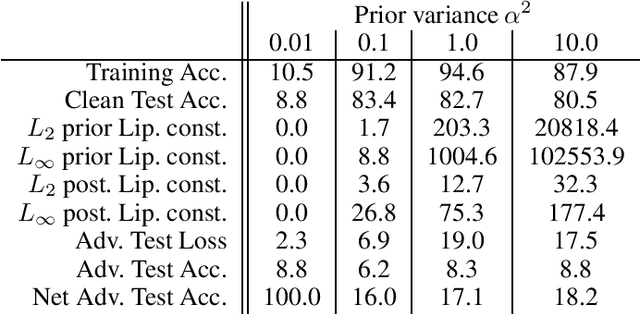
It is desirable, and often a necessity, for machine learning models to be robust against adversarial attacks. This is particularly true for Bayesian models, as they are well-suited for safety-critical applications, in which adversarial attacks can have catastrophic outcomes. In this work, we take a deeper look at the adversarial robustness of Bayesian Neural Networks (BNNs). In particular, we consider whether the adversarial robustness of a BNN can be increased by model choices, particularly the Lipschitz continuity induced by the prior. Conducting in-depth analysis on the case of i.i.d., zero-mean Gaussian priors and posteriors approximated via mean-field variational inference, we find evidence that adversarial robustness is indeed sensitive to the prior variance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge