The Devils in the Point Clouds: Studying the Robustness of Point Cloud Convolutions

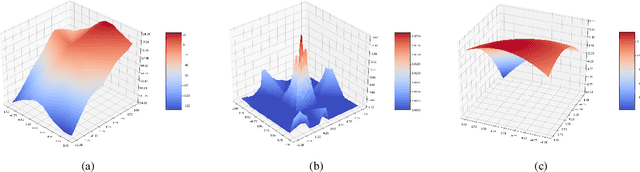
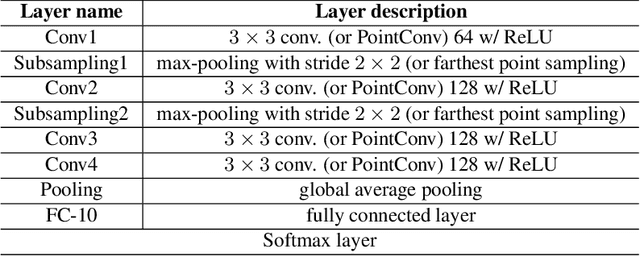
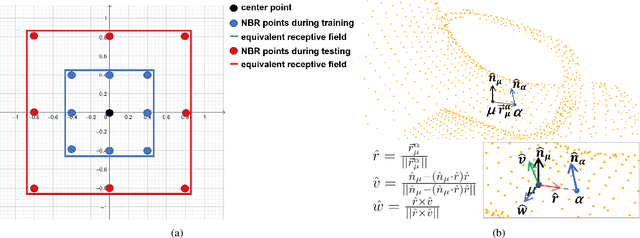
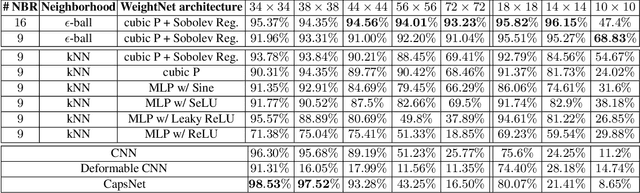
Recently, there has been a significant interest in performing convolution over irregularly sampled point clouds. Since point clouds are very different from regular raster images, it is imperative to study the generalization of the convolution networks more closely, especially their robustness under variations in scale and rotations of the input data. This paper investigates different variants of PointConv, a convolution network on point clouds, to examine their robustness to input scale and rotation changes. Of the variants we explored, two are novel and generated significant improvements. The first is replacing the multilayer perceptron based weight function with much simpler third degree polynomials, together with a Sobolev norm regularization. Secondly, for 3D datasets, we derive a novel viewpoint-invariant descriptor by utilizing 3D geometric properties as the input to PointConv, in addition to the regular 3D coordinates. We have also explored choices of activation functions, neighborhood, and subsampling methods. Experiments are conducted on the 2D MNIST & CIFAR-10 datasets as well as the 3D SemanticKITTI & ScanNet datasets. Results reveal that on 2D, using third degree polynomials greatly improves PointConv's robustness to scale changes and rotations, even surpassing traditional 2D CNNs for the MNIST dataset. On 3D datasets, the novel viewpoint-invariant descriptor significantly improves the performance as well as robustness of PointConv. We achieve the state-of-the-art semantic segmentation performance on the SemanticKITTI dataset, as well as comparable performance with the current highest framework on the ScanNet dataset among point-based approaches.