The Complex Gaussian Kernel LMS algorithm
Paper and Code
May 06, 2010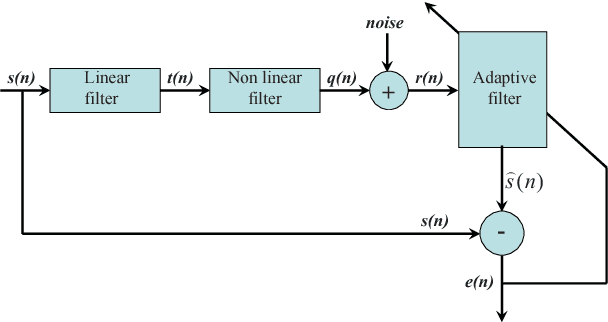
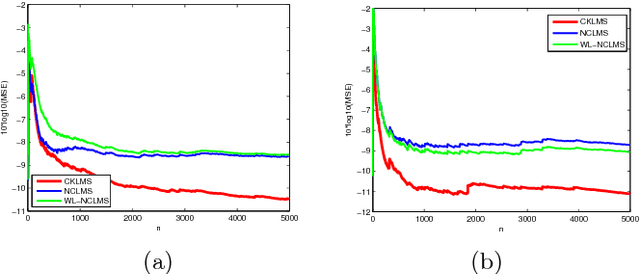
Although the real reproducing kernels are used in an increasing number of machine learning problems, complex kernels have not, yet, been used, in spite of their potential interest in applications such as communications. In this work, we focus our attention on the complex gaussian kernel and its possible application in the complex Kernel LMS algorithm. In order to derive the gradients needed to develop the complex kernel LMS (CKLMS), we employ the powerful tool of Wirtinger's Calculus, which has recently attracted much attention in the signal processing community. Writinger's calculus simplifies computations and offers an elegant tool for treating complex signals. To this end, the notion of Writinger's calculus is extended to include complex RKHSs. Experiments verify that the CKLMS offers significant performance improvements over the traditional complex LMS or Widely Linear complex LMS (WL-LMS) algorithms, when dealing with nonlinearities.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge