The Cellwise Minimum Covariance Determinant Estimator

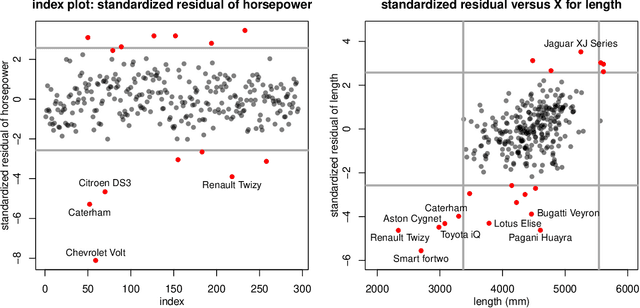
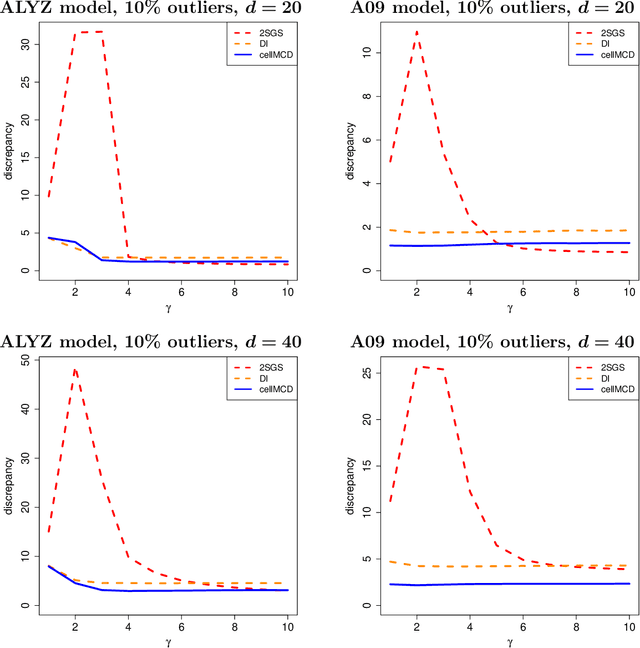
The usual Minimum Covariance Determinant (MCD) estimator of a covariance matrix is robust against casewise outliers. These are cases (that is, rows of the data matrix) that behave differently from the majority of cases, raising suspicion that they might belong to a different population. On the other hand, cellwise outliers are individual cells in the data matrix. When a row contains one or more outlying cells, the other cells in the same row still contain useful information that we wish to preserve. We propose a cellwise robust version of the MCD method, called cellMCD. Its main building blocks are observed likelihood and a sparsity penalty on the number of flagged cellwise outliers. It possesses good breakdown properties. We construct a fast algorithm for cellMCD based on concentration steps (C-steps) that always lower the objective. The method performs well in simulations with cellwise outliers, and has high finite-sample efficiency on clean data. It is illustrated on real data with visualizations of the results.