The Block Point Process Model for Continuous-Time Event-Based Dynamic Networks

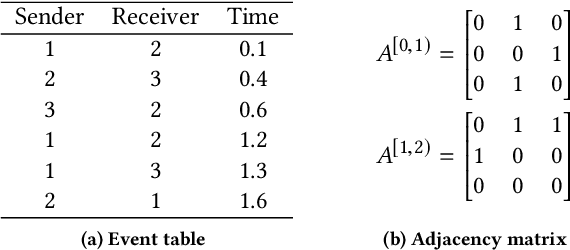
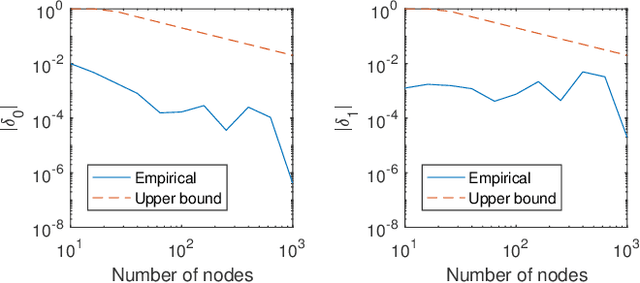
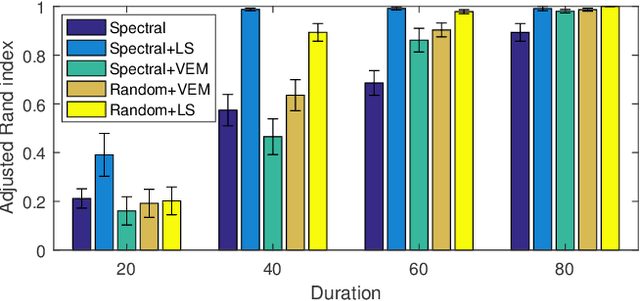
Many application settings involve the analysis of timestamped relations or events between a set of entities, e.g. messages between users of an on-line social network. Static and discrete-time network models are typically used as analysis tools in these settings; however, they discard a significant amount of information by aggregating events over time to form network snapshots. In this paper, we introduce a block point process model (BPPM) for dynamic networks evolving in continuous time in the form of events at irregular time intervals. The BPPM is inspired by the well-known stochastic block model (SBM) for static networks and is a simpler version of the recently-proposed Hawkes infinite relational model (IRM). We show that networks generated by the BPPM follow an SBM in the limit of a growing number of nodes and leverage this property to develop an efficient inference procedure for the BPPM. We fit the BPPM to several real network data sets, including a Facebook network with over 3, 500 nodes and 130, 000 events, several orders of magnitude larger than the Hawkes IRM and other existing point process network models.