Temporally Folded Convolutional Neural Networks for Sequence Forecasting
Paper and Code
Jan 10, 2020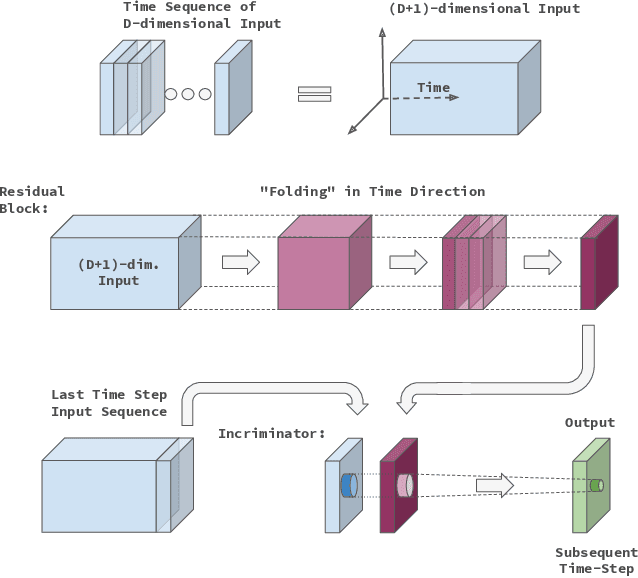
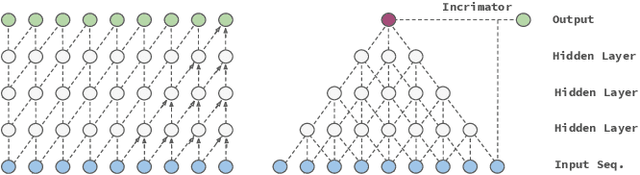
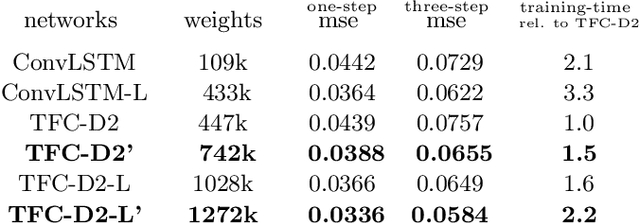

In this work we propose a novel approach to utilize convolutional neural networks for time series forecasting. The time direction of the sequential data with spatial dimensions $D=1,2$ is considered democratically as the input of a spatiotemporal $(D+1)$-dimensional convolutional neural network. Latter then reduces the data stream from $D +1 \to D$ dimensions followed by an incriminator cell which uses this information to forecast the subsequent time step. We empirically compare this strategy to convolutional LSTM's and LSTM's on their performance on the sequential MNIST and the JSB chorals dataset, respectively. We conclude that temporally folded convolutional neural networks (TFC's) may outperform the conventional recurrent strategies.
* 8 pages, 4 figures, submitted to IJCAI 2020 Proceedings
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge