Take it in your stride: Do we need striding in CNNs?
Paper and Code
Dec 07, 2017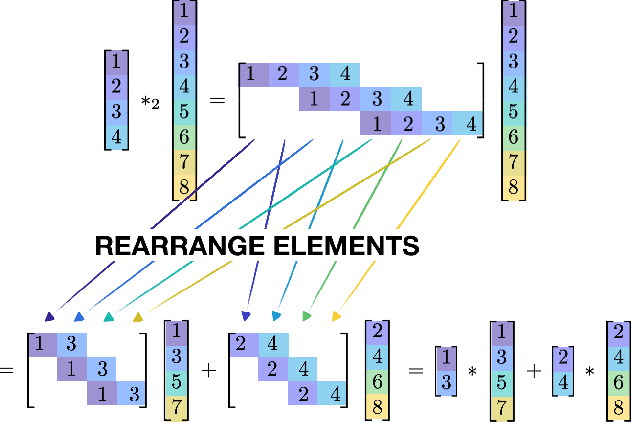

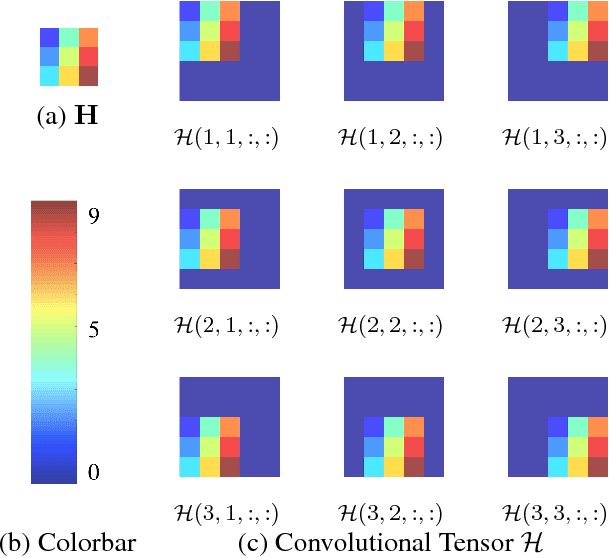

Since their inception, CNNs have utilized some type of striding operator to reduce the overlap of receptive fields and spatial dimensions. Although having clear heuristic motivations (i.e. lowering the number of parameters to learn) the mathematical role of striding within CNN learning remains unclear. This paper offers a novel and mathematical rigorous perspective on the role of the striding operator within modern CNNs. Specifically, we demonstrate theoretically that one can always represent a CNN that incorporates striding with an equivalent non-striding CNN which has more filters and smaller size. Through this equivalence we are then able to characterize striding as an additional mechanism for parameter sharing among channels, thus reducing training complexity. Finally, the framework presented in this paper offers a new mathematical perspective on the role of striding which we hope shall facilitate and simplify the future theoretical analysis of CNNs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge